Recursion in Java

What is Recursion in Java?

The process of making a function call itself is known as recursion. With the use of this strategy, complex problems can be reduced to more manageable, simpler ones.

Recursion could be a little challenging to comprehend. Experimenting with it is the most effective way to learn how it functions.

Pseudo-code

Syntax of Recursion in Java

Every recursive code in programming must have a condition that stops the recursion. If the condition is not provided or not given correctly it will lead to stack overflow error.

Let's see an example where we can stop the recursion using a base condition:

Output:

How Recursion Works?

Let us understand the working of recursion using a problem statement.

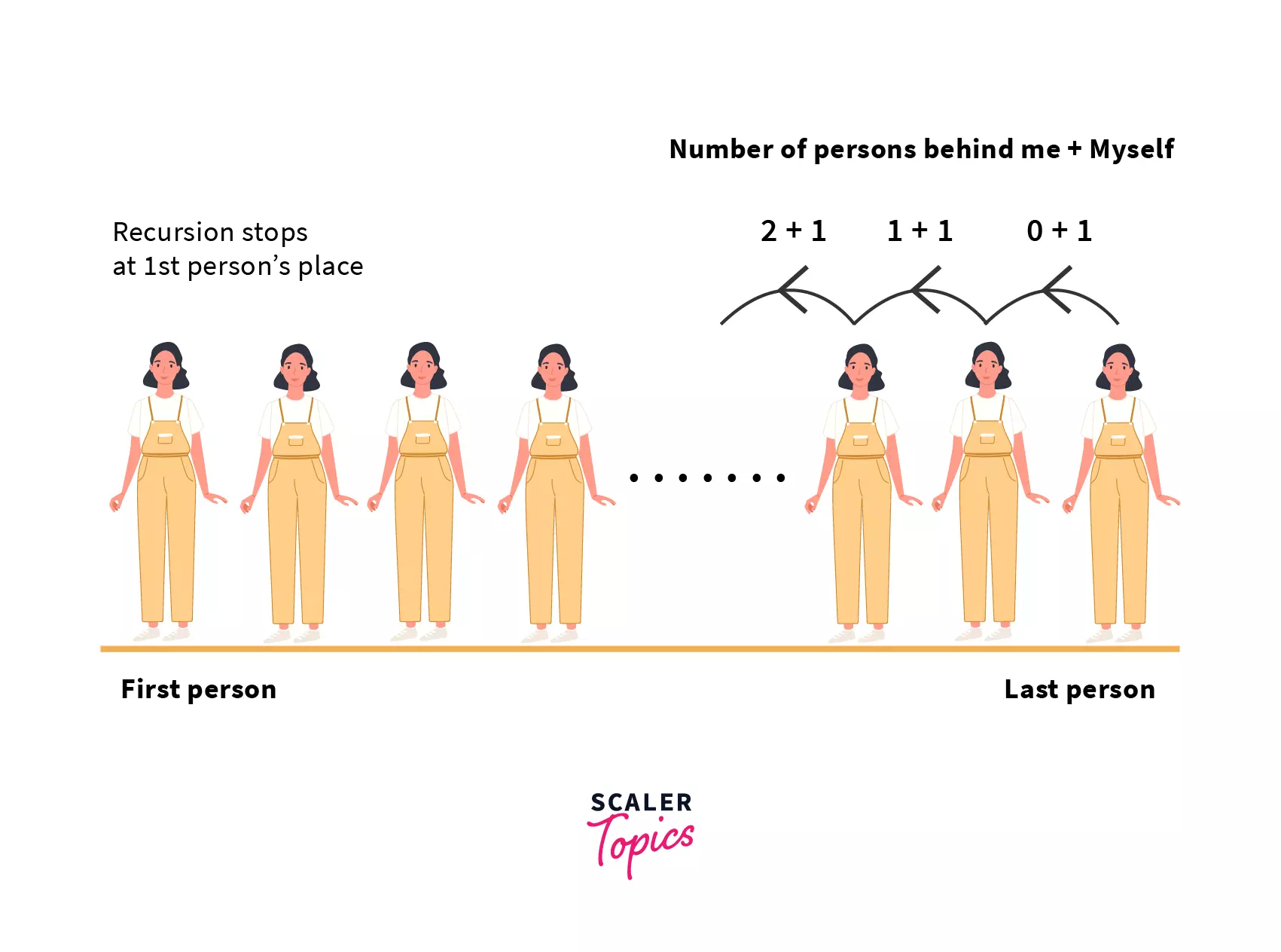
• You are asked to count the the total number of people in the queue without leaving your place, where you are standing at first place in a queue of N number of people.
• You turn to look behind you to check if anyone is there. If not, you can respond with "0" as your response. Repeat this action if someone is present, then watch for their response as you stand back.
• After receiving a response, a person adds 1 for the person behind them before answering the questioner or the person in front of them.

The picture below shows how recursion works. At each recursive step, some computation is performed

Code for counting the total number of persons.

Output:

Explanation:

• As we can see in the above code snippet, the count function is calling itself. The above program runs until the number is not equal to the number assigned to the first person.
• Everytime we call the recursive function we decrease the counter of currentPerson by one and increase the counter of countTillNow by one.

What is the Base Condition of Recursion?

The base condition of any recursive function signifies the smallest sub-problem, which further cannot be broken into any sub-problem. If the base condition is not provided or not given properly the recusrion will run infinitely causing stack overflow error.

Let us find the sum of numbers up to 20 using recursion in java.

Code

Output:

Explanation:

In the above code snippet, we can see the base case. If the value of i equals 1, then the function returns 1. In any other cases, we call the recursive function, and every time we call the recursive function, we decrease the value of i by 1 and increase the currSum by i. So, if the value of i is one, the recursive function gets terminated.

Stack Overflow Error in Recursion

Let us understand the stack overflow error from the example taken above, i.e., finding the sum up to 20. We have defined the base condition; if the value of i is equal to 1, then it returns 1, and hence recursion will break or else recursion continues. What if we replace the base condition with the following code:

Output:

After executing the program, it will display a stack overflow error as recursion will never reach the base case because we decrease the value of i by 1 every time. Hence call stack memory will get exhausted by these method calls, and an error occurs.

Example of Recursion in Java

1. Infinite recursion

Infinite recursion occurs only when the base case is not achieved or is not defined. In such cases, the recursive calls are made to themselves, and this leads to a stack overflow error.

Code

Output

Explanation

When we make a call to print function, it will continuously call itself because no base case is applied, and hence it runs infinitely.

2. Palindrome Number Program

Palindrome number: A palindromic number is a number that remains the same when its digits are reversed. For example 1234321 is palindrome number because if we reverse it will generate the same number, but 2331 is not a palindrome number because reversing it will generate 1332, which is not the same.

Let us see a program to check whether the number is palindrome or not using recursion in Java.

Code

Output:

Explanation:

• In the above example, we first took a number and passed it into a function called palindrome. We have converted an integer number to a string in the palindrome function.
• Now we pass the string into the checkPalindrome function. The checkPalindrome takes three arguments, i.e., the input string s, left pointer, and right pointer.
• The recursive function checkPalindrome traverses the string from both sides, from left and right. We provide two base cases.

First base case: If the left pointer has a value greater than or equal to the value of the right pointer implies that we have traversed till the middle of the string, and the string is a palindrome. Hence, we return true value to the recursive function.

Second base case: If at any point s[left] is not equal to s[right], then we return false because the number will not be a palindrome as the left part is not the same as the right part. If both the base cases are skipped, it will make a recursive call. Every time we make a recursive call, we will decrease the right pointer by 1 and increase the left pointer by 1.

3. Factorial Number Program

Factorial: Factorial of any number n is the product of all the numbers from 1 to n. For example, the factorial of a number 5 will be product of 1,2,3,4,5, i.e., 120. (can be written as 5! = 120) Let us write a program to find factorial of a number using recursion in Java.

Code

Output

Explanation

• In the above code, the recursive function factorial takes an integer as a parameter. The base case for the factorial function is: if the value of n is zero, then return 1.
• If the value of n is not zero, then call the factorial recursively and decrease the value of n by 1.
• We are returning n * factorial(n - 1) because the factorial of a number x will be the product of x and the factorial of x-1. x! = x * (x - 1)!.

4. Fibonacci Series Program

Fibonacco series: If F(n) denotes the nth Fibonacci number then F(n) can be written as F(n - 1) + F(n - 2). Let us understand the Fibonacci series by an example. Let the first two terms of the Fibonacci series be 1 and 1. The third term will be the sum of previous terms according to the standard definition. So the third term will be 1 + 1 = 2. In this way, the pattern will be continued. The following image will show how to calculate the further terms. Let us generate the Fibonacci series using recursion in Java.

Code

Output

Explanation

• In the above code, the recursive function fibonacci takes an integer as a parameter. The base case for the fibonacci function is: if the value of n is greater than or equal to zero, then return n.
• If the value of n is not zero, then call the fibonacci function recursively. We make recursive calls as fibonacci(n-1) + fibonacci(n-2) because F(n) = F(n - 1) + F(n - 2).

5. Binary Search using Recursion

Binary search is a searching algorithm with the least time complexity among all the search algorithms with one condition - the container or list must be sorted. If the element is present in the array, we have to return the element's index from the array or else return -1.

In a binary search algorithm, we divide the array into two parts. Check if the middle element is greater than the target element; if so, just continue searching in the right half of the array. If the middle element is smaller than the key element, we continue searching in the left half of the array. This works because the array is sorted.

So the total complexity of the binary search algorithm is n * log(n) (n is the size of a sorted array). The time complexity will be logarithmic because after every recursive call we discard half of the array.

Code

Output

Explanation

In the above code, the binarySearch function takes four parameters, i.e., array, left pointer(l), right pointer(r), and the key element to be found(num).

There are two base conditions they are as follows:

1. If the left pointer is greater than the right pointer, the function returns -1 (It implies that the key element is not found in the array).
2. If arr[mid] is equal to key element return mid (It implies that the key element is present in the array).

If the two base conditions are failed, then we will compare the key element with the arr[mid] where mid represents the middle element in the array arr. If arr[mid] is greater than the key element, we will make a recursive call for the left half of the array, and if it's smaller, it will make a recursive call for the right half of the array.

Types of Recursion

There are two types of recursion based on when the recursive call is made to function.

Tail Recursion

When the last statement in the recursive method is the recursive call for that function, it is termed tail recursion. There is no further execution of any code after calling the recursive call. The recursive call is usually made along with the return statement.

Syntax (Pseudocode) for the tail recursion in Java:

In the above article, the program of fibonacci series is an example of tail recursion.

Head Recursion

If the first statement in the recursive method is the recursive call, it is head recursion. There’s no statement, no operation before the call. The function doesn't perform any operations at the time of calling, it will perform all the operationa at the time of returning.

Syntax for the head recursion in Java:

In the above article, the program of binary search is an example of head recursion.

Advantages of Recursion

• Writing iterative approaches is quite a difficult task as it requires a lot of implementation, whereas recursive approaches are very small to code.
• It is very useful in traversal techniques (Depth first search, Breadth first search, Inorder/Postorder/Pre-order tree traversals, etc.) where normal iteration is hard to implement.

Disadvantages of Recursion

• It is very difficult to trace recursion, which is why it is very hard to debug.
• Recursion uses a lot of stack memory as well as processor time.
• The machine may run out of memory if recursive calls are not written properly.
• It is hard to understand the code, as visualizing it is a tedious task.