Quick Sort in C Program

What is Quick Sort in C?

• In C programming language, Quick Sort is a Sorting algorithm, which uses Divide and Conquer Approach to perform sorting.
• Quick Sort is the most efficient algorithm among all other sorting algorithms, as sorting can be done in O(n*logn) time.
• The Initial step of the Quick Sort algorithm is to select the pivot element and then rearrange the elements around the pivot element. A pivot can be any element in the array or a pivot can be the first or last element of the array or it could either be the median of the array.

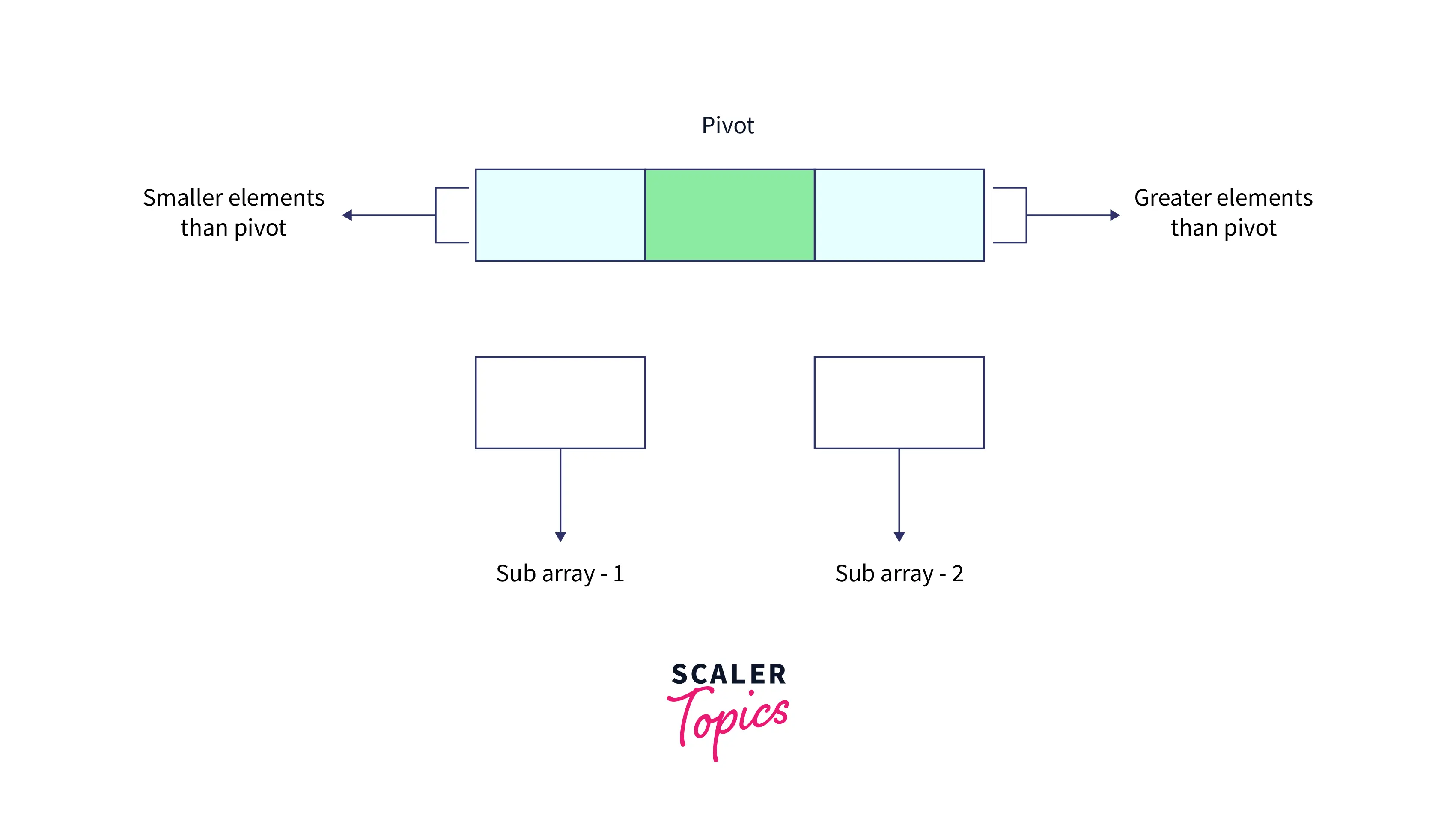
• After selecting the pivot element, we would rearrange the array elements and then split the array into two sub-arrays such that all sub-array 1 contains array elements that are lesser than the pivot while sub-array 2 contains array elements greater than the pivot.
• Interesting thing about the Quick Sort algorithm is that the chosen pivot element would be placed at the exact index position where it should be in the sorted array because all elements to its left are less than the pivot element and all elements to its right are greater than it.
• Each sub-array is further divided until each sub-array contains only a single array element. Then we will combine all such sub-arrays to form a single sorted array.
• For a better understanding of the Quick Sort algorithm, Assume this, your group of friends went for a trip, and now its time to capture a group photo, to ensure that the image looks good and to make everyone visible in the photograph, all of your friends must stand height wise, here Instead of photographer telling everyone to stand at a particular position by comparing every one’s height, all of your friends can stand at a position because everyone knows their own height. For example, the tallest guy knows were to stand and the medium guy knows where to stand. In a similar way, each one of you friends can stand by comparing their own height with others.
• Similarly, In the Quick Sort algorithm every array element arranges itself by comparing its value with others to sort the given array. So, the pivot element would be placed exactly at its sorted position. Thereby, sub-arrays are divided around the pivot element.

Working of Quick Sort Algorithm in C

The execution of the quick sort c program starts from the main function, before we actually call the quick sort function, we define the size of the array and array elements

Pivot: Pivot is an element that is selected by an algorithm to perform calculations

Step 1: Initial step in the algorithm is to select a Pivot element, Generally we have the flexibility to choose the pivot element as a first element or last element or median element or any random element. For more efficiency, the Last element of the array is picked as the pivot, so let’s consider the last element as the pivot.

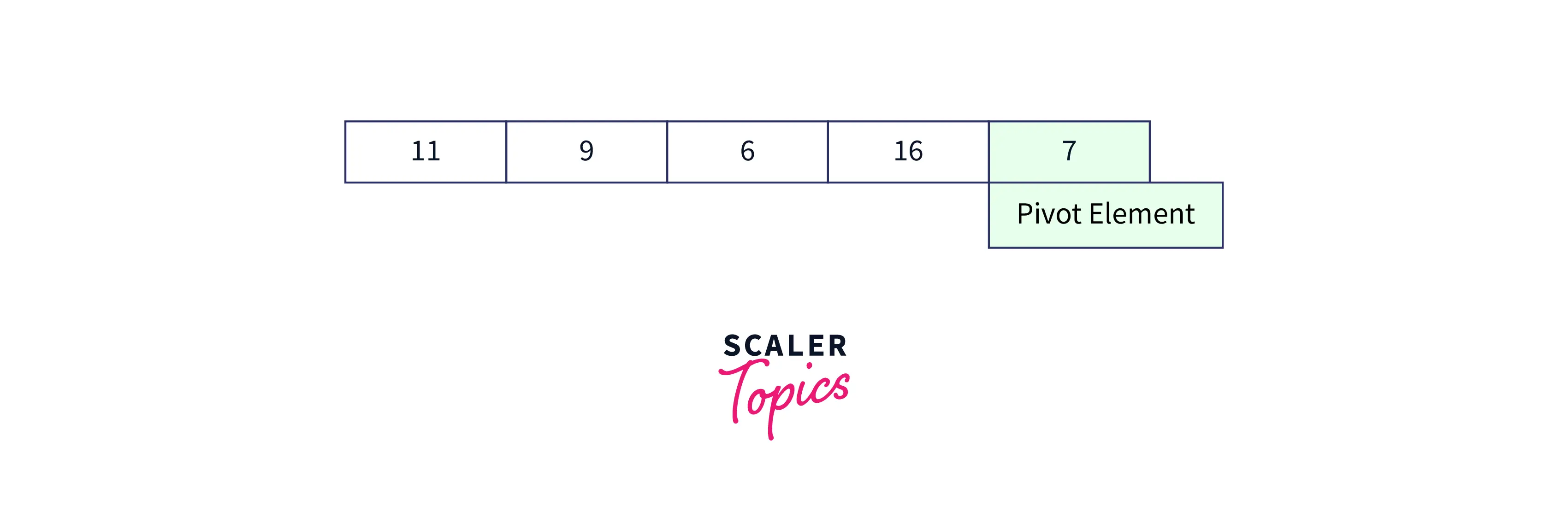
Step 2: In this step, we need to partition the array elements in such a way that elements smaller than the pivot are placed to the left side of the pivot while the elements greater than the pivot are placed to the right side of the pivot. Please note that at this step elements need not be sorted. The array would look like the below image after rearranging.

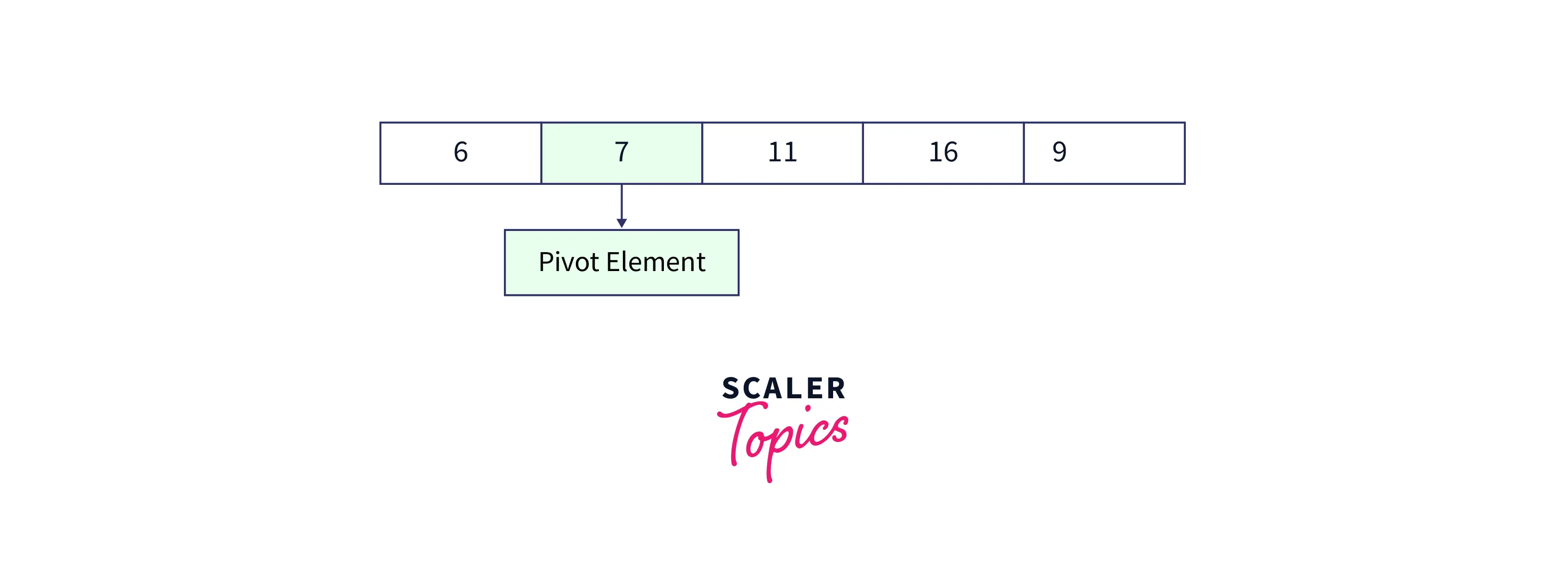
Now we have partition the array, let us understand the actual process of rearrangement:

• Let us take two variables i, and j, Here i variable is used for swapping while the j variable is used for iterating over array elements. Elements less than the pivot are to be stored till ith position.
• Let us initialize the 0th index as low and the last index of the array as high, note that we will be traversing the array till high-1.

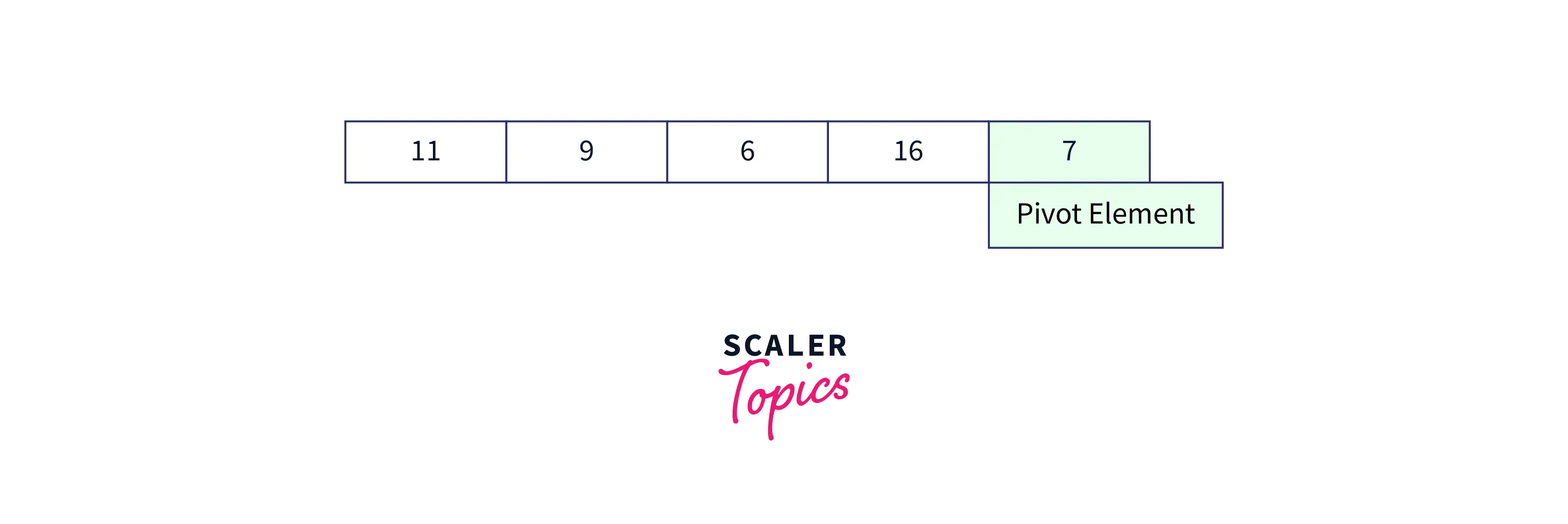
• Now, initialize the i,j variables as i=low-1, j=0.

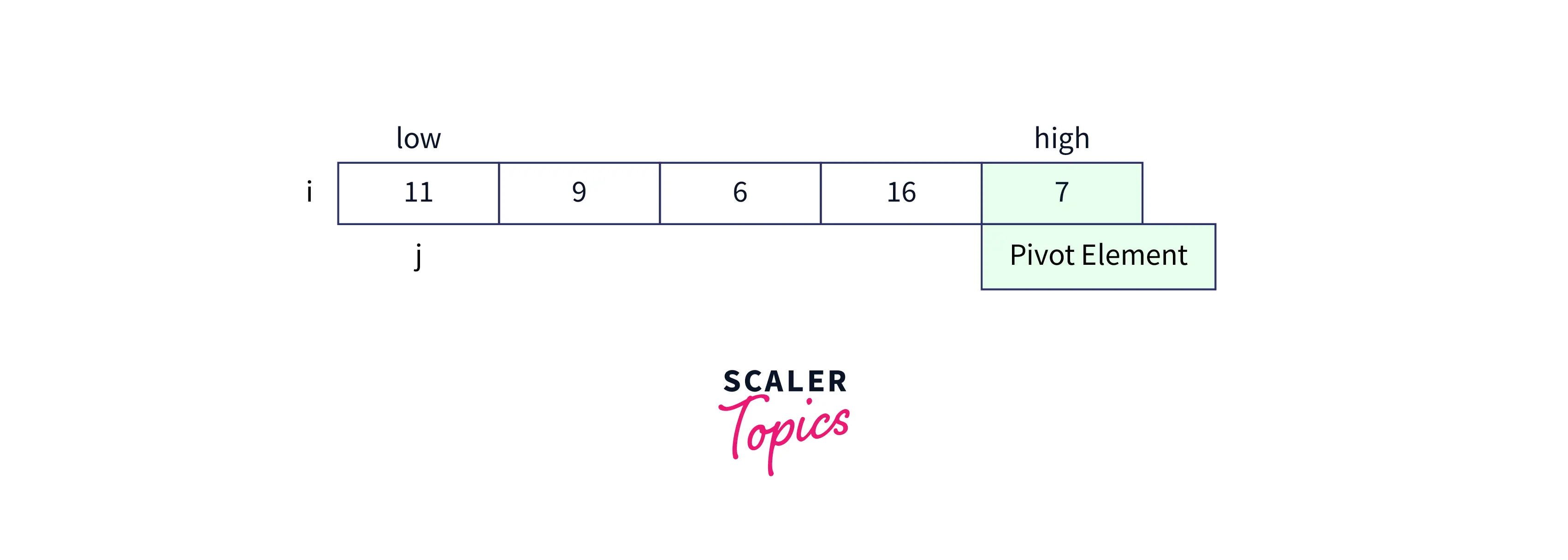
• Compare the value at index j and pivot, if the value at index j is less than the pivot then increase the value of i and perform a swap operation for i and j. As the current jth index element 11 is not less than the pivot element 7, we do not perform a swap operation and increments the j value to move to the next index element.

  

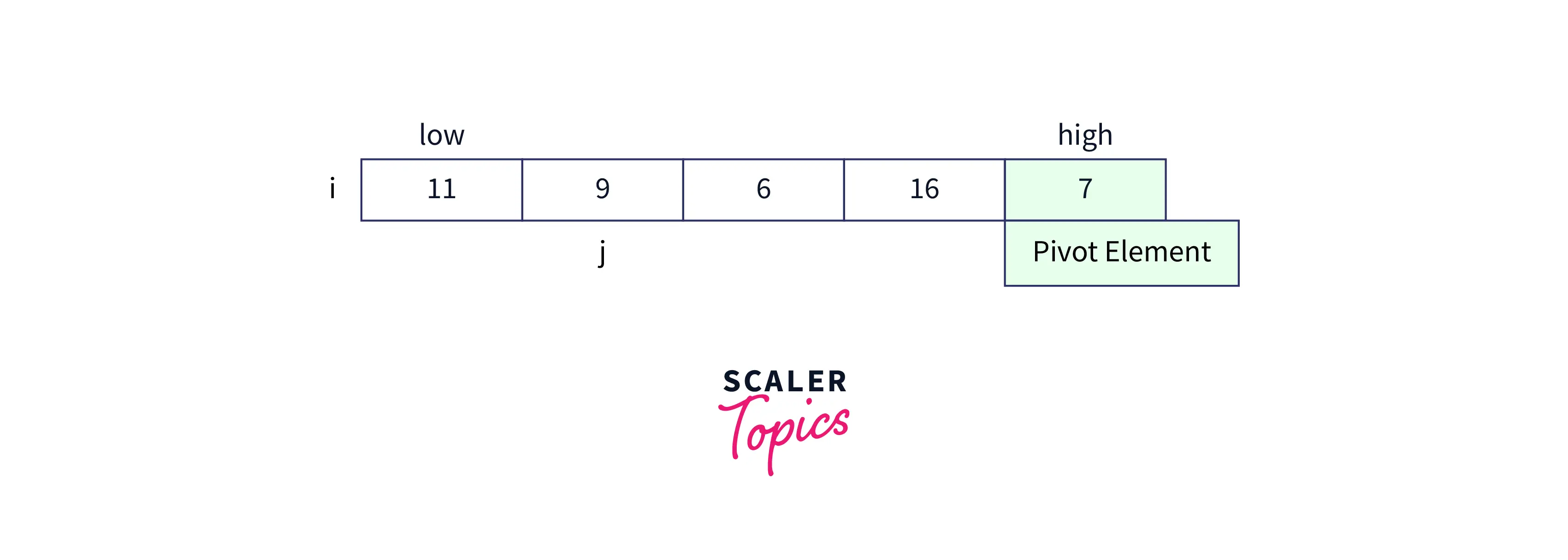
• Now again compare the value at index j and the value of the pivot element, since 9 is not less than 7 we don’t perform any swap and simply increment the value of j to move to the next index.

  

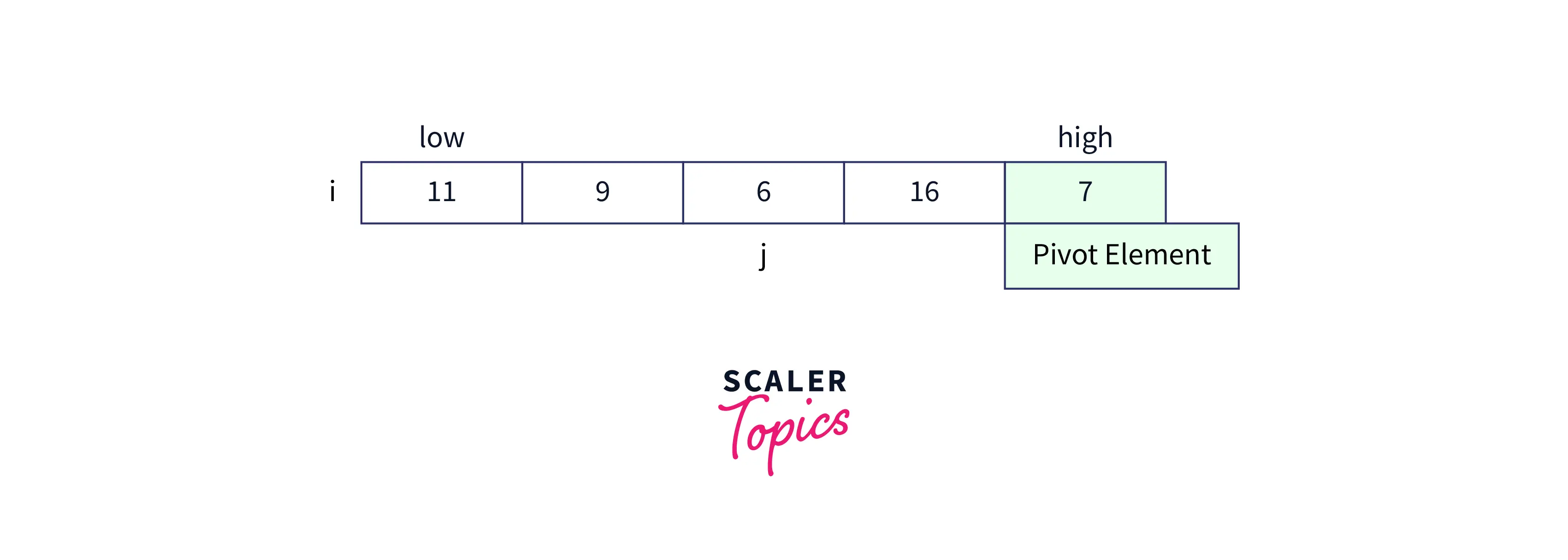
• Now the value at the jth index i.e 6 is less than the value of pivot element 7. So, we perform a swap operation, by increasing the ith index and performing a swap between the ith index and the jth index.

fig: After performing the swap operation array would look like the above image.

• Let us compare the value at the jth index with the value at the pivot element, since 16 is not less than 7 we do not perform any swap operation.

• Here comes our last step of the partition, now increment the value of i and swap ith index element with the pivot element.

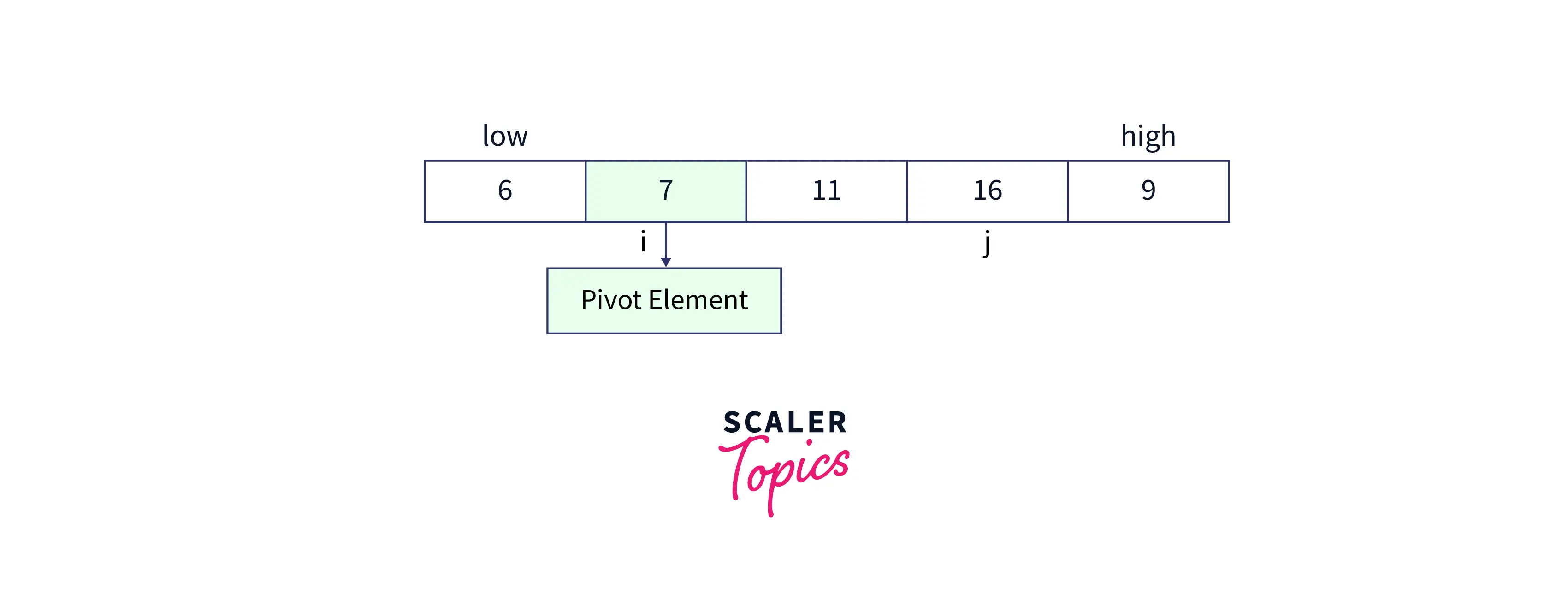
• Observe that all the elements to the left side of the pivot are lesser than the pivot while all the elements to the right side of the pivot are greater than the pivot. This is the actual process of rearranging the elements around the pivot. Kindly take a moment to visualize the process as it would be beneficial while writing the code for the Quick Sort c program.

Step 3: In this step, the entire array divides into two sub-arrays, i.e. sub-array-1 as elements before the pivot element and sub-array-2 as elements after the pivot element.

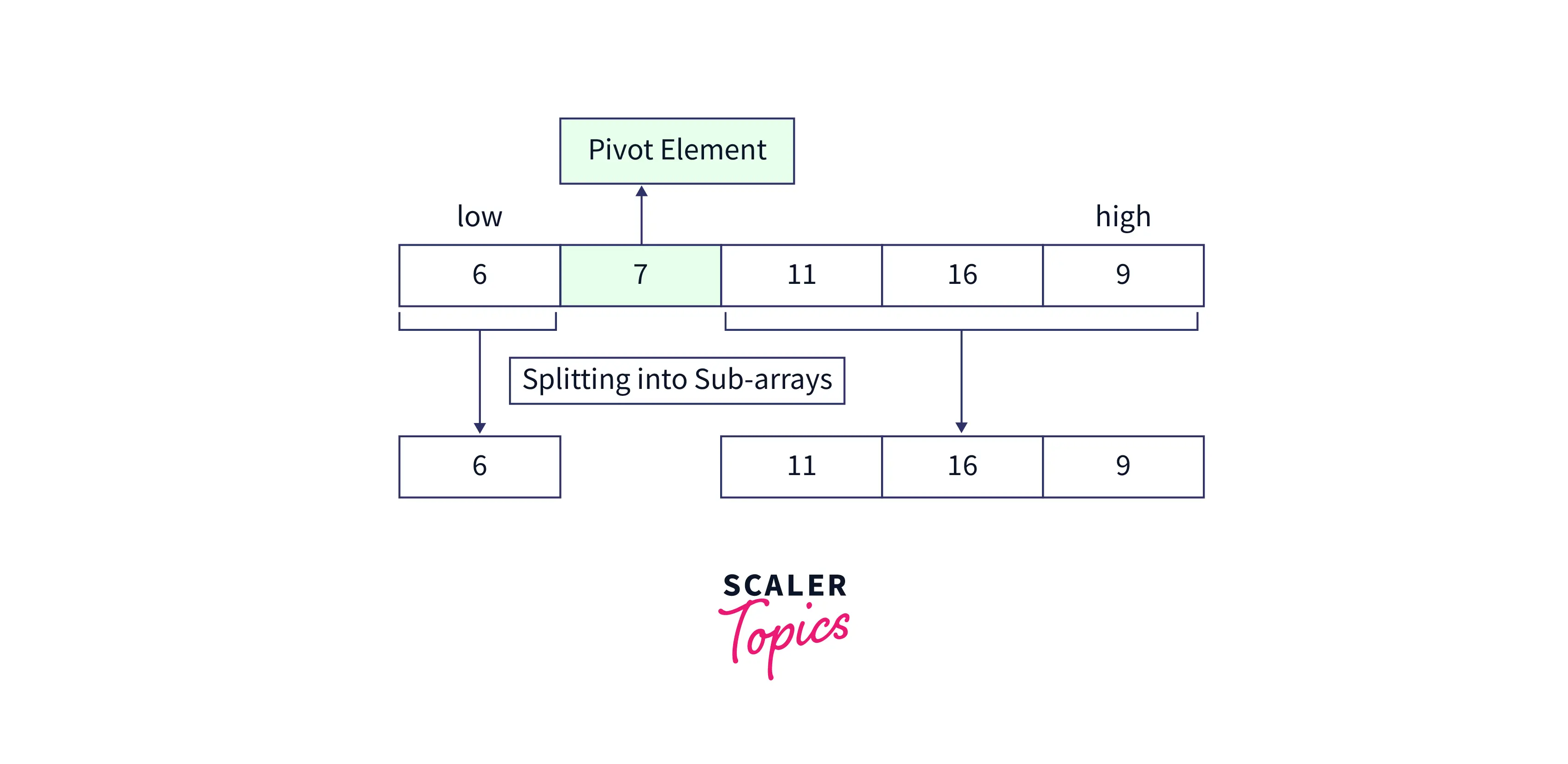
• I hope by this time, you might have gained a good understanding of the algorithm

Step 4: This step is very simple, repeat the above-discussed steps for every sub-array till both the whole array get sorted.

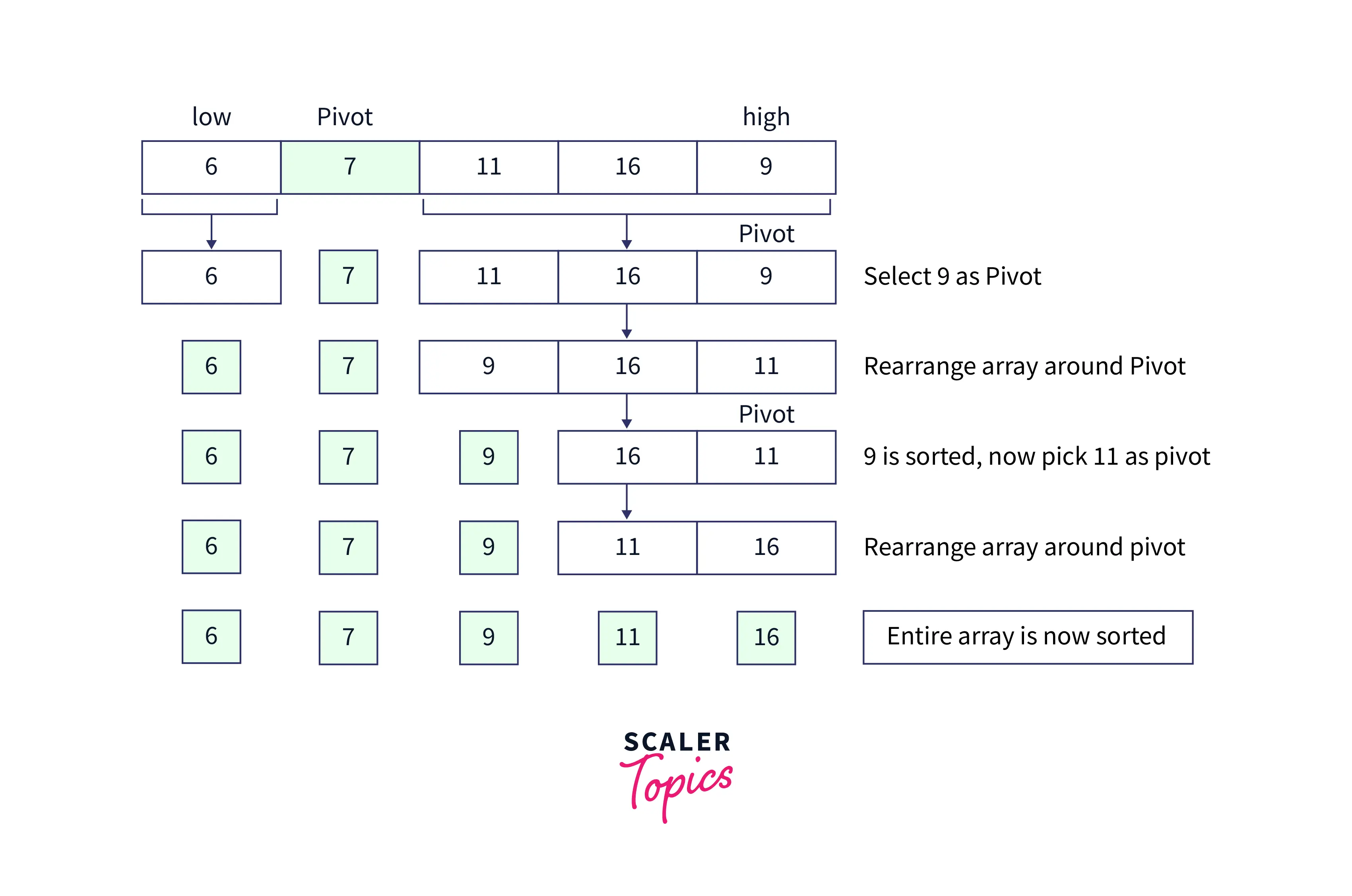As the sub-arrays are now sorted this makes the entire array as a sorted array.

Pseudocodes for QuickSort Algorithm

Pseudocode Function for Partition Function

Partition function will divide the array according to the pivot and returned the correct index of the pivot element.

Pseudocode Function for Quick Sort Function

Complexity Analysis of Quick Sort Algorithm

A. Time Complexity

Best Case

In the Quick Sort algorithm, if the position of the pivot element is in the middle of the array and if we perform partition in the middle of the array it leads to best case performance.

For an Instance, Let us consider an array of n elements we will divide(partition) this array from the middle such that every partition contains at most n/2 elements, and continue this partition until each subarray contains only one element.

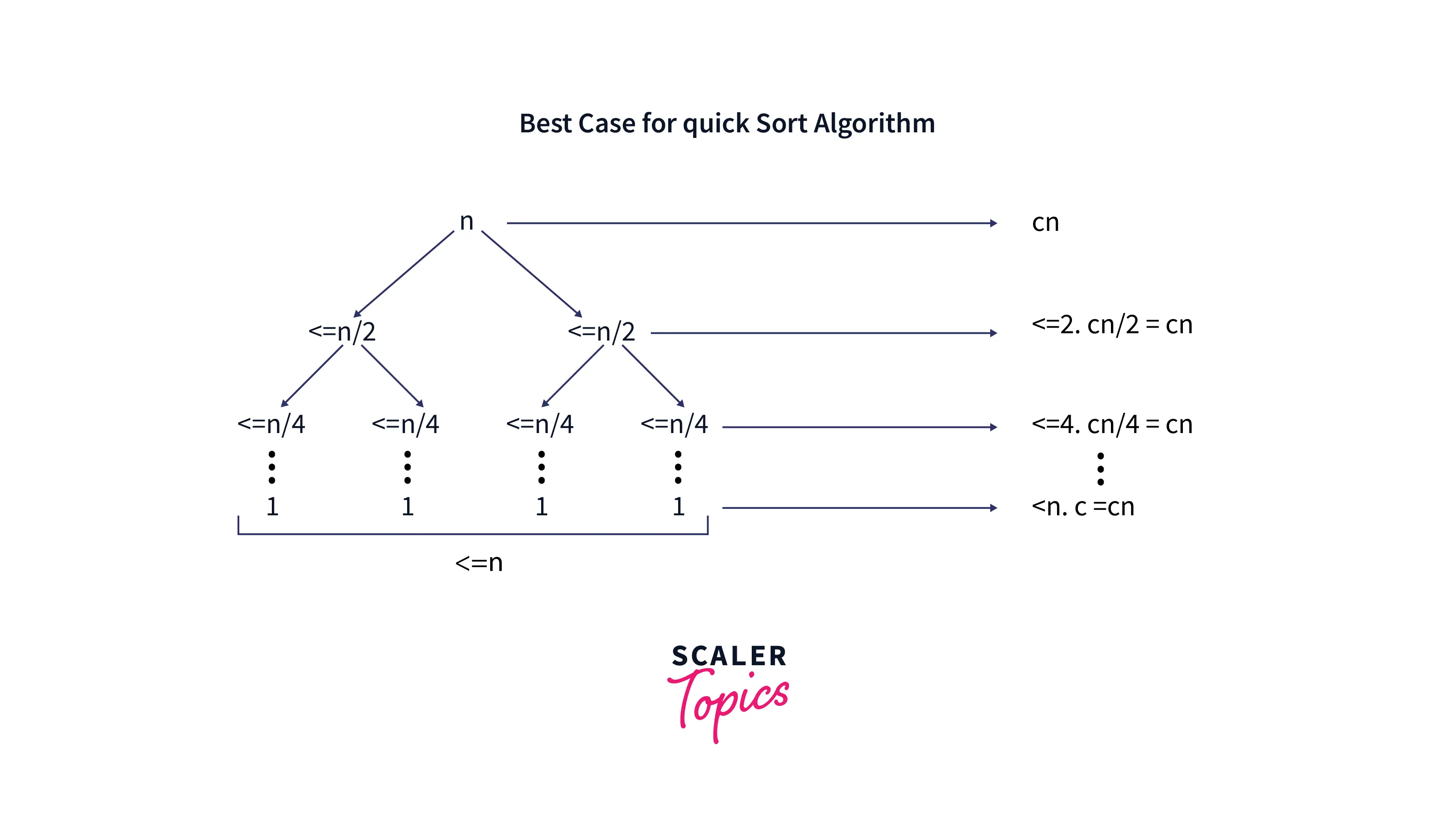
The above image is the representation of a binary tree, and the height of a binary tree is equal to logn. Therefore the complexity of this part is O(logn). As we are iterating over the array for the rearrangement of elements around the pivot element, the time complexity of the partition() function would be O(n). So, we can conclude that O(nlogn) is the best-case time complexity for the Quick Sort algorithm.

Worst Case

In Quick Sort algorithm, if the partition is made in such a way that it is unbalanced, then the Worst Case situation occurs. This unbalanced partition occurs if the smallest or largest element is selected as the pivot.

In this situation, the location of the pivot element would be at the end of the array, so when the partition is performed one sub-array would be always empty while the other sub-array would contain n-1 elements. So, for the first call, the two subarrays would contain 0 & n-1 elements respectively, while for second call subarrays would contain 0 & n-2 elements respectively, this process continues till only one element is left. So time complexity would be computed as the sum of all complexities at each step. The number of steps are n and for every step O(n) time is required so the time complexity of the worst case is O(n*n). Refer to the below image for the tree representation of this condition.

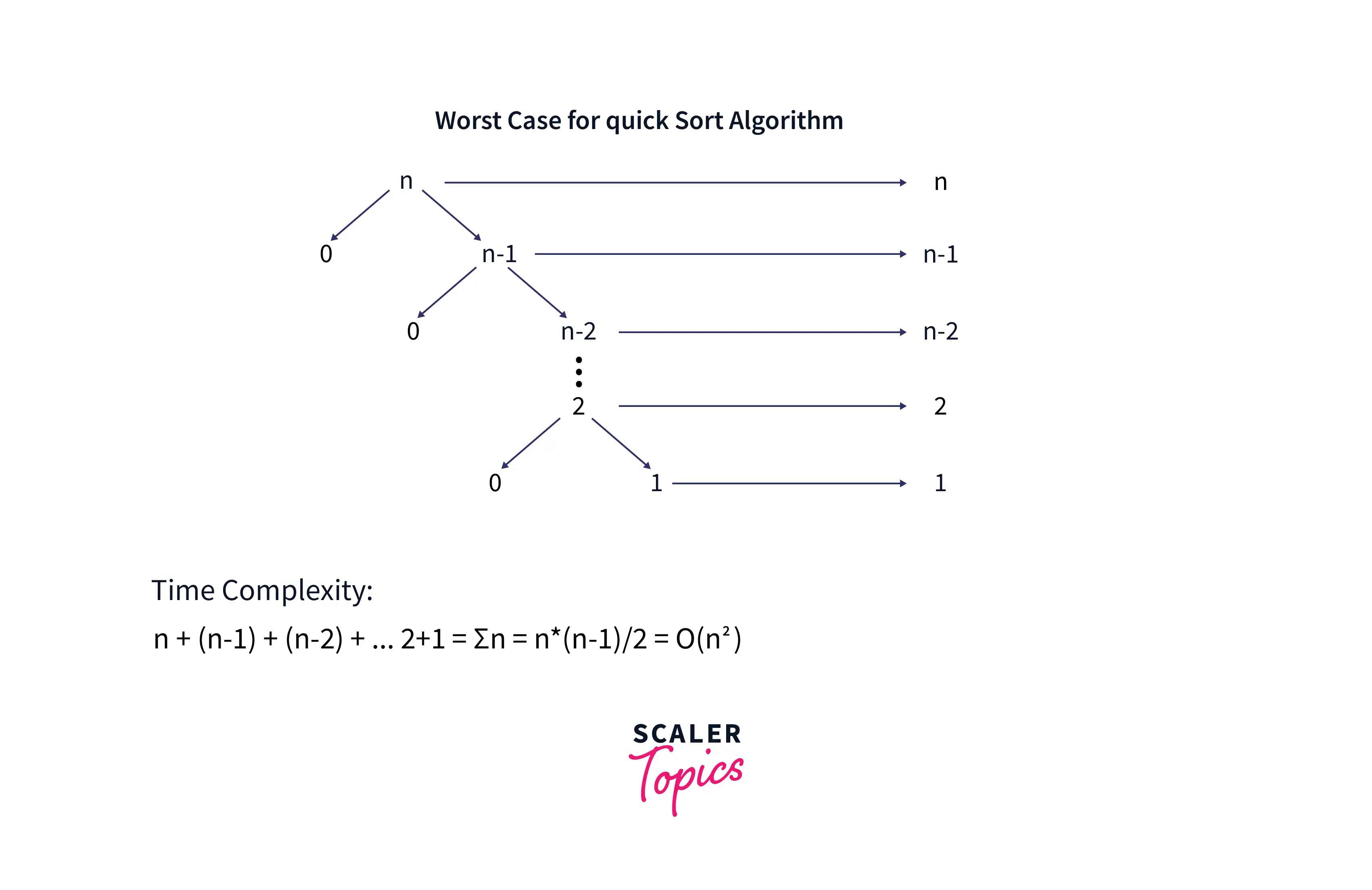
B. Space Complexity

In the Quick Sort algorithm, the space occupied by Recursion Stack is used for calculating Space Complexity. In the Worst Case Scenario, the space complexity of the Quick Sort algorithm in O(n) as n recursive calls will be made. Average space complexity for Quick Sort algorithm is O(log n).

C Program for Quick Sort in Recursive Mode

Output:

Let us understand the above recursive implementation of the Quick Sort Algorithm: The execution of the program starts from the main function, we declared the size of the array and array elements. Now we are calling the quicksort function which in turn calls the partition function and rearranges the array elements around the pivot element and returns the partition index to the quicksort function, now quick sort function again calls itself to sort the elements which are lesser than the pivot, after this quicksort function calls itself to sort the elements which are greater than the pivot. In the above code, we also have a swap function which is used by partition function to swap the jth index with the ith index element. Finally, in the main function, we print the sorted array using for a loop.

C Program for Quick Sort in Iterative Mode

Output:

Let us understand the above Iterative implementation of the Quick Sort Algorithm:

The flow of the program starts from the main function, we defined the array elements and called the quicksort function which creates a temporary array that will act as a stack in this case by replacing the recursion stack. Then Quick Sort function uses a while loop to get the sorted index position of the partition element in the array, quicksort function itself calls the partition function to get the index of the sorted pivot element (partition function rearranges the array elements around the pivot). Quick Sort function uses this partition index and checks if there any elements to the left side if yes then it adds the low, pi-1 indexes to the array so we could implement the quick sort function in the quick sort c program to that sub-array later using this stack. Then it checks if there are any elements to the right side of the partition index, if yes, then it adds pi+1, high index to the array. Then by using these index values we go for another iteration in while loop until the entire array is sorted.

When is the Quick Sort Algorithm Used?

• Quick Sort is mostly used when the stable sort is not required
  • Stable Sort: If the relative order of two equal elements is preserved after sorting, such an algorithm is called as a stable sort.
• Quick Sort algorithm is mostly used where Time complexity matters.
• Quick Sort algorithm is mostly used where Space complexity matters.
• Quick Sort algorithm is used if the programming language is suitable for recursion.