Level Order Traversal
Video Tutorial
Overview
Level order traversal of a tree is a breadth-first traversal where nodes at a given depth are printed together, and all such levels are displayed in different lines.
Scope of Article
This article discusses the level order traversal algorithm and its intuition, as well as its code implementation in C++ and Python.
This article assumes that the reader knows about the breadth-first search (BFS) algorithm.
Takeaways
- Complexity of Level order traversal
- Time complexity -
Introduction
Suppose you're given a family tree drawn on paper and you want to know all your cousins' names. So what do you do?
First, you find your name in the chart. Since your cousins belong to the same level of hierarchy as you in the family tree, you move your finger/pointer horizontally parallel to the base of the family tree chart.
All the names (or nodes) you cross during your horizontal movement are your cousins!
The operation/traversal you just performed is what is called the level traversal of a tree for a given level . In general, the level order traversal of a tree consists of these level traversals for all valid values of .
Read the section below to find how a level is defined for a tree.
Problem Statement
Given an n-ary tree's root node, print all the nodes in a level order fashion, with each level displayed on a separate line. In each level, the data of valid nodes should be printed separated by space.
Note
- Tree: An undirected and acyclic graph
- N-Ary Tree: A tree in which each node can have up to N child nodes
- Level of node: Level of a node in a tree is defined as the number of edges present between the node and the root of the tree. By definition, the root node is considered to be present at level 0.
See the example case below for a better understanding.
Example Case:
Suppose a tree is given as follows:
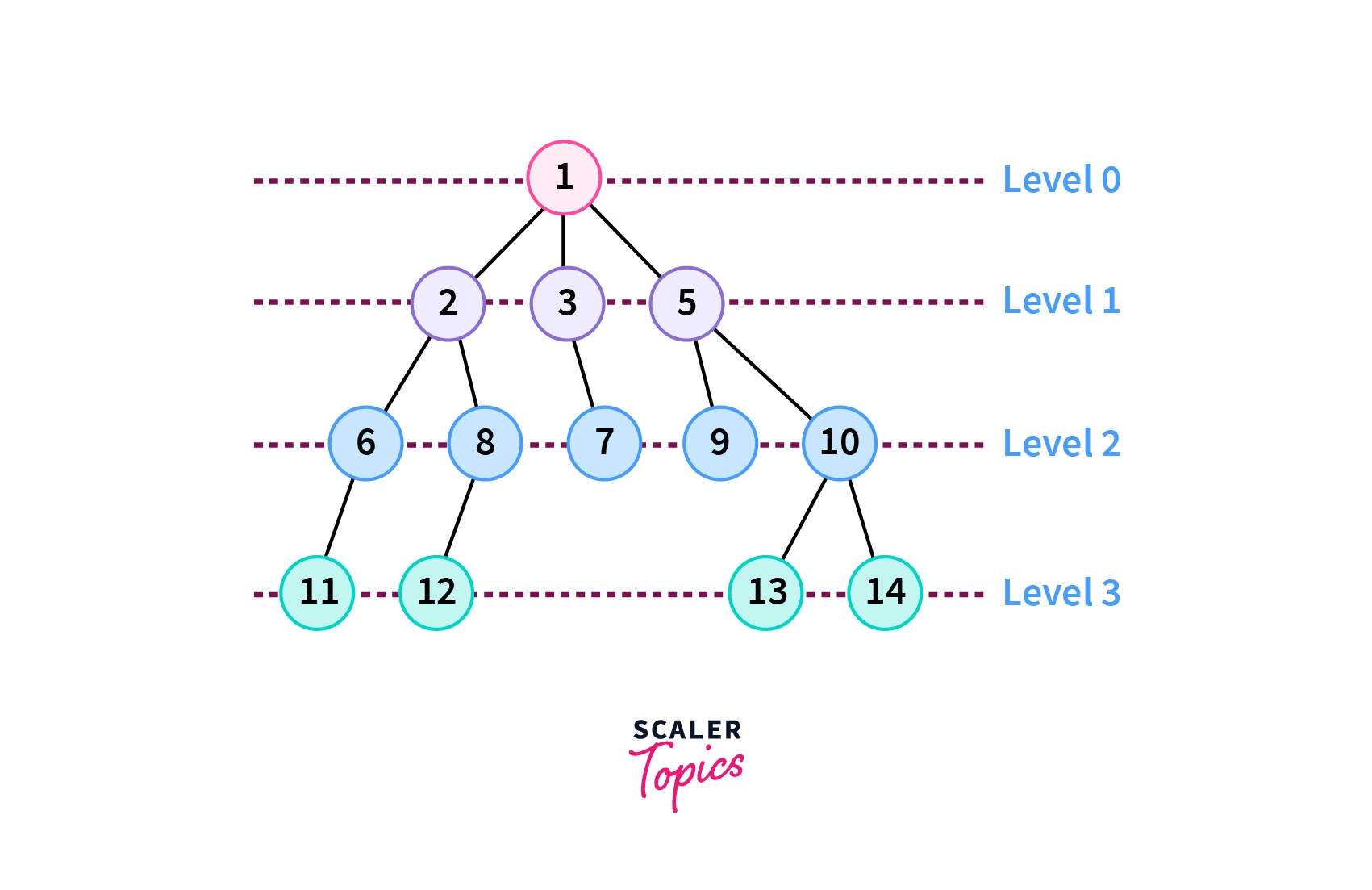
The level order traversal of this tree will be as follows:
Explanation:
- Since 1 is the root node, it is present at level 0 and is printed first.
- The nodes 2, 3, 5 have 1 edge between themselves and the root node, and hence are present at level 1, and are printed together.
- Similarly, the nodes (6, 8, 7, 9, 10) are present at level 2, and the nodes (11, 12, 13, 14) are present at level 3.
Algorithm
1. Intuition
Before explicitly defining the algorithm, we should work a little bit on intuition.
-
At first glance this problem seems awfully similar to the BFS problem/algorithm. And it should since all trees are also graphs.
-
If it had been a simple BFS, then the output would have been in a single line. For example, in the tree shown above, the output of a BFS traversal would have been
1 2 3 5 6 8 7 9 10 11 12 13 14
-
Clearly, we need to do some additional tweaks to our standard BFS algorithm to take into account the shift into the next level of the tree.
-
While applying BFS, we make use of a queue data structure. We start with the root node and push its children nodes into the queue. One by one we pop the front of the queue and push the children of that node (just popped from the queue) into the queue.
-
Now, while pushing the nodes' children, we also have to put some sort of an indicator into the queue when all the nodes at a particular level are exhausted.
Now, how to achieve this? Suppose we have a value called LevelEnd which indicates that the nodes of a current level have been exhausted and we should print the upcoming nodes in a new line.
When do we know a given level has been exhausted? It's pretty simple. When all the nodes in the previous level get processed, all their children are in the queue. Once all the child nodes are in the queue, we can put the LevelEnd value in the queue to represent that this is the end of this level.
Take the above tree as an example.
- When {1} is processed, {2, 3, 5} are present in the queue (Level 0 exhausted)
- When {2, 3, 5} are processed, {6, 8, 7, 9, 10} are enqueued. (Level 1 exhausted)
and so on...
Making use of this observation, let us define our algorithm.
2. Designing The Algorithm
Input: Root of an n-ary tree
Output: Nodes of the tree printed in level order fashion
Algorithm:
- Initialize a queue with the root node and then push the LevelEhe programs given above, first, we initialize a queue using the root node and LevelEnd value.
- In the case of C++, nullptr acted as LevelEnd value while in case Python None did.
- Until the queue is not empty, nodes were processed one by one.
- In each iteration, the front of the queue was popped. If the front of the queue was the LevelEnd value, then a new line was printed.nd value
- Repeat until the queue is empty: a. Pop the front value from the queue. Let's call it front_node b. If front_node is not the same as LevelEnd, then print the value present in the node c. Else, check if the queue is empty or not. If it is empty, break out the loop. d. Otherwise, print a new line and pushLevelEnd into the queue and continue.
Note:
The LevelEnd value is just an indication of a new line and should not be a valid node in the tree. We have total independence of what value we consider as LevelEnd.
For example, in Python, we can use None. Suppose the tree consisted of only positive integer values, we could also consider, say -1, as the LevelEnd.
On the other hand, in C++, since the queue will be of TreeNode* type, we have to use the nullptr or NULL value as LevelEnd.
Approches
Approach 1 : Level Order Traversal using Recursion
To perform a level order traversal of a binary tree using recursion in C++, you can utilize a queue data structure. The algorithm works as follows:
- Create a queue and enqueue the root node. While the queue is not empty, perform the following steps:
- Dequeue a node from the front of the queue.
- Process the dequeued node (print its value or perform any desired operation).
- Enqueue its left child (if it exists).
- Enqueue its right child (if it exists).
- Repeat steps 2 until the queue becomes empty.
Here's the C++ code implementation for level order traversal using recursion:
1. C++ Implementation
Complexity Analysis: The complexity analysis of the level order traversal algorithm using recursion in a binary tree can be broken down as follows:
Time Complexity:
- Enqueuing and dequeuing each node takes constant time O(1).
- In the worst case, all nodes in the binary tree need to be processed, resulting in a total of N nodes being processed.
- Therefore, the time complexity of the level order traversal algorithm is O(N), where N is the number of nodes in the binary tree.
Space Complexity:
- The space complexity is determined by the queue used to store the nodes during the traversal.
- In the worst case, the queue can contain all the nodes at a particular level of the binary tree.
- The maximum number of nodes that can be present at any level is the maximum number of nodes at the leaf level, which is N/2 (approximately).
- Therefore, the space complexity of the algorithm is O(N).
- It's important to note that although the algorithm uses recursion, it doesn't rely on recursion for the traversal itself. The recursion is only used to enqueue nodes and traverse the binary tree in a level order manner.
Approach 2 : Level Order Traversal For A Binary Tree using Queue
Here's the basic algorithm for level order traversal using a queue:
- Create a queue of nodes.
- Enqueue the root node of the binary tree.
- Start a loop until the queue becomes empty.
- Dequeue a node from the front of the queue.
- Process the dequeued node (print its value or perform any desired operation).
- Enqueue the left child of the dequeued node (if it exists).
- Enqueue the right child of the dequeued node (if it exists).
- End of loop.
- Done.
This algorithm performs a breadth-first search traversal of the binary tree, visiting each node level by level. 1. C++ Implementation
Complexity Analysis:
Time Complexity:
- Enqueuing and dequeuing each node takes constant time O(1).
- In the worst case, all nodes in the binary tree need to be processed, resulting in a total of N nodes being processed.
- Therefore, the time complexity of the level order traversal algorithm is O(N), where N is the number of nodes in the binary tree.
Space Complexity:
- The space complexity is determined by the queue used to store the nodes during the traversal.
- In the worst case, the queue can contain all the nodes at a particular level of the binary tree, which can be at most N/2 nodes (in the case of a complete binary tree at the last level).
- Therefore, the space complexity of the algorithm is O(N), where N is the number of nodes in the binary tree.
- The level order traversal using a queue offers a time complexity of O(N) and a space complexity of O(N), where N is the number of nodes in the binary tree.
Example of Level Order Traversal
We will be taking the same tree we described above for our example to demonstrate the algorithm of level order traversal. Here is the tree diagram again.
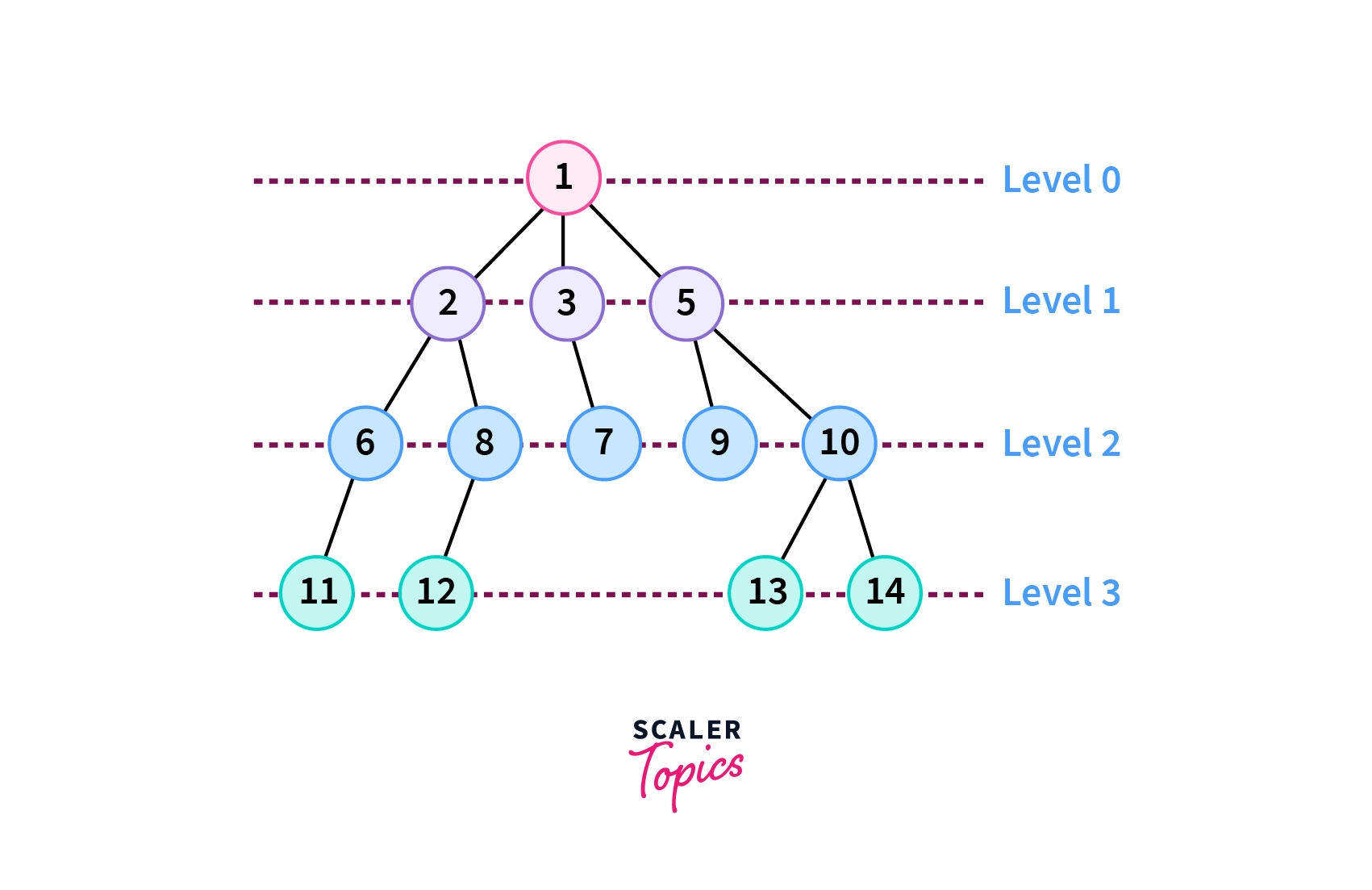
We will be using the 𝜙 character to denote the LevelEnd value.
Step 0:
Initialize an empty queue.
Step 1:
Append the root and the LevelEnd value in the queue.
| 1 | 𝜙 |
|---|
Step 2:
Take out the front of the queue, that is, 1.
Since it is not LevelEnd, we print the value and push its child nodes into the queue.
Output:
Queue:
| 𝜙 | 2 | 3 | 5 |
|---|
Step 3:
Take out the front of the queue, which in this case is 𝜙, that is, the LevelEnd value. Now according to the program/algorithm, we need to print a new line.
Also, since the queue is not empty, we need to push 𝜙 into the queue. Therefore,
Output:
Queue:
| 2 | 3 | 5 | 𝜙 |
|---|
Similarly, Last Step:
Output:
Queue:
Space & Time Complexity
Space Complexity: Since no more than nodes will be present in the queue at any given time, we can assume that the worst-case complexity is of order , that is:
Time Complexity: Since all nodes are processed only once, therefore, we can say that if the number of nodes is , then the time complexity of the level order traversal algorithm is of the order:
Conclusion
- Level Order Traversal is very similar to breadth-first search algorithm/traversal with different level nodes being printed on different lines
- The level order traversal also makes use of a queue data structure (just like in BFS)
- Additionally, we need to make use of a LevelEnd in the queue to indicate that all the nodes in a given level have been exhausted
- In the case of Python, we use None as LevelEnd, while in C++ we use nullptr.
- Both the time and space complexity of level order traversal is
