Factorial of a Number in C

Why do we need factorial?

Suppose you have four boxes of different colors, and you have to arrange them in random order. You can order the boxes like this –

Or like this –

Or maybe like this –

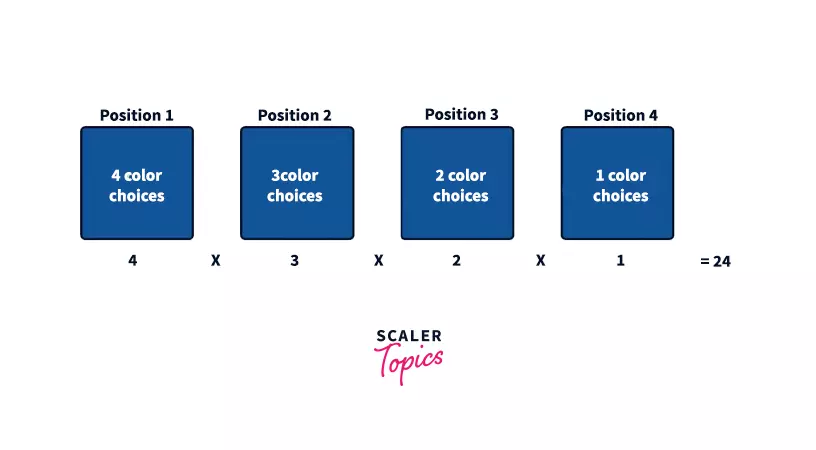
But what if you have to find the total number of patterns in which you can arrange these boxes? You can do it by the following method –

Step 1: Pick the first location at which we can place the box. For this, we have four color choices to fill the position. We have red, green, blue, and yellow colors with us.

Step 2: Pick the second location and place a box over there. We can choose any color from the remaining three colors since we only have three color choices.

Step 3: Pick the third location in the order and place a box from the remaining ones. For this, we can choose from the remaining two colors.

Step 4: For the last location, we only have one color left. So, we will fill the fourth position with the only color left with us.

Step 5: To get the number of all possible patterns, multiply the values obtained in each of the above steps i.e. 4 x 3 x 2 x 1 = 24.

Therefore, there are 24 possible orders in which you can arrange these boxes.

Doing such a long process could be tedious and time-consuming sometimes. Therefore, we have an alternative for this known as Factorials. They are denoted by ‘!’ (exclamation mark).

By definition, the factorial of a number n is the multiplication of all the numbers ranging between n and 1. Therefore factorial(n) = n.(n-1).(n-2)………….3.2.1. Some of the examples of factorials are –

5! = 5 x 4 x 3 x 2 x 1 = 120 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720

Now that we have understood what factorials are, we will now see how to calculate the factorial of a number in C. In this article, we will cover the following approaches to compute factorial in C –

1. Compute the factorial of a number in C using a for-loop.
2. Compute the factorial of a number in C using recursion.
3. Compute the factorial of a number in C using a ternary operator.
4. Compute the factorial of a number in C using the tgamma() method.

Algorithm to compute factorial of a number in C

Step 1: Take input from the user. Let’s name this variable n.

Step 2: Starting from n, keep decreasing its value till n becomes 1 and multiply the value obtained in each step. To make it simpler –

1. Start with n, decrease its value by 1 and multiply it to n that is n.(n – 1). Store the value thus obtained in a variable called fact.
2. Take n – 1, again decrease its value by 1 and multiply it to the last value of the variable fact that is fact. (n – 2) = n. (n – 1). (n – 2).
3. Repeat the above steps till n becomes 1 that is n. (n – 1). (n – 2)…..3.2.1 Step 3: Print the value of the variable fact.

Compute the factorial of a number in C using a for loop

In this approach to calculate the factorial of a number, we will use a for loop. Suppose we want to calculate the factorial of 3. To do this, we have to start from 1 and keep on multiplying till 3 that is 1 * 2 * 3.

We can do this easily by a for loop, where we initialize a variable i = 1, and will increase the value of i in each iteration by 1, until 3. Under the loop, we will multiply the value of i obtained in each iteration and save it in a variable. The final value of the variable would be the factorial.

In this case, for the first iteration, we will have a value of i equal to 1, 2 for second and 3 for third. Multiplying all these values will give us the factorial of 3 that is 6 (1 x 2 x 3).

Output –

To understand the above C program, let us study the flow –

1. Declare a variable, n in the main() function

2. Ask the user to input the number n to calculate its factorial. Let it be 3.

3. Pass the value obtained from the user n to the factorial(n) function.

4. In the factorial(n) function –

• Initialize variables fact = 1 and i = 1
• Run a for loop from i = 1 till i <= n i.e. from 1 till 3.
• Under the loop – Perform the operation: fact = fact * i. Here we are multiplying the value of i to the value of fact upon each iteration of the loop. This way, we are multiplying the numbers starting from 1 till the number n (3 in this case). 1st iteration: fact = 1 * 1 = 1

2nd iteration: fact = 1 * 2 = 2

3rd iteration: fact = 2 * 3 = 6

• Return the value of fact (6 in this case).

5. Print the value returned from the factorial() function.

This program takes a positive integer from the user and computes the factorial using a for loop. The time complexity of the above code is O(n) time since the loop executes n times, so the sequence of statements also executes n times.

Compute the factorial of a number in C using Recursion

A function that calls itself is known as a recursive function. And this technique of calling a function is known as recursion. In recursion, we split a function into smaller versions of the function itself. Each time the function makes a call to itself, an updated value is passed as an argument.

If we want to calculate the factorial of a number using recursion, the function factorial() should make a call to itself by passing a value which is less than the previous value by 1 till we reach the value 1. In other words, if we start calling the function factorial() with the value n, the function should call itself with the value n – 1 all the way till 1. And with each call of the function, we should keep on multiplying the values to calculate the factorial.

The recursion continues till a condition is encountered that prevents it, referred to as the base condition.

Now, how do we calculate the factorial of a number by using recursion?

Consider we have a function called factorial(n), which takes n as a parameter. To call the function recursively, we must have –

1. A condition that stops the recursion (Base Condition).
2. A part that calls the same function (factorial in this case). Upon each call, the function should recursively call itself by decreasing the number n by 1.

Observe the code –

Consider passing n = 3 to the factorial(n) function. Each function multiplies the number n with the factorial of the number below it (n – 1) until it is equal to one. The following is the flow of recursive calls –

This way, we can keep on calling the factorial(n) function recursively until n becomes 0 to compute the factorial of a given number.

Now, let us understand the flow of the given program –

1. Declare a variable, n in the main() function.
2. Ask the user to input the number, n to calculate its factorial. Let it be 3.
3. Pass the value obtained from the user n to the factorial(n) function.
4. In the factorial(n) function –

• Place a condition that returns 1 if the value of n is equal to 0.

• Return n * factorial(n – 1). We start from number n (3 in this case) and move till the number 1 while multiplying the value gained by performing the operation factorial(n – 1) in each function call till the value of n becomes 0. 1st function call: factorial(3) = 3 * factorial(2)

  2nd function call: factorial(2) = 2 * factorial(1)

  3rd function call: factorial(1) = 1 * factorial(0)

  4th function call: factorial(0) = 1 (since n has now become 0 and according to our condition the function will return 1)

5. Print the value returned from the factorial() function i.e. 6.

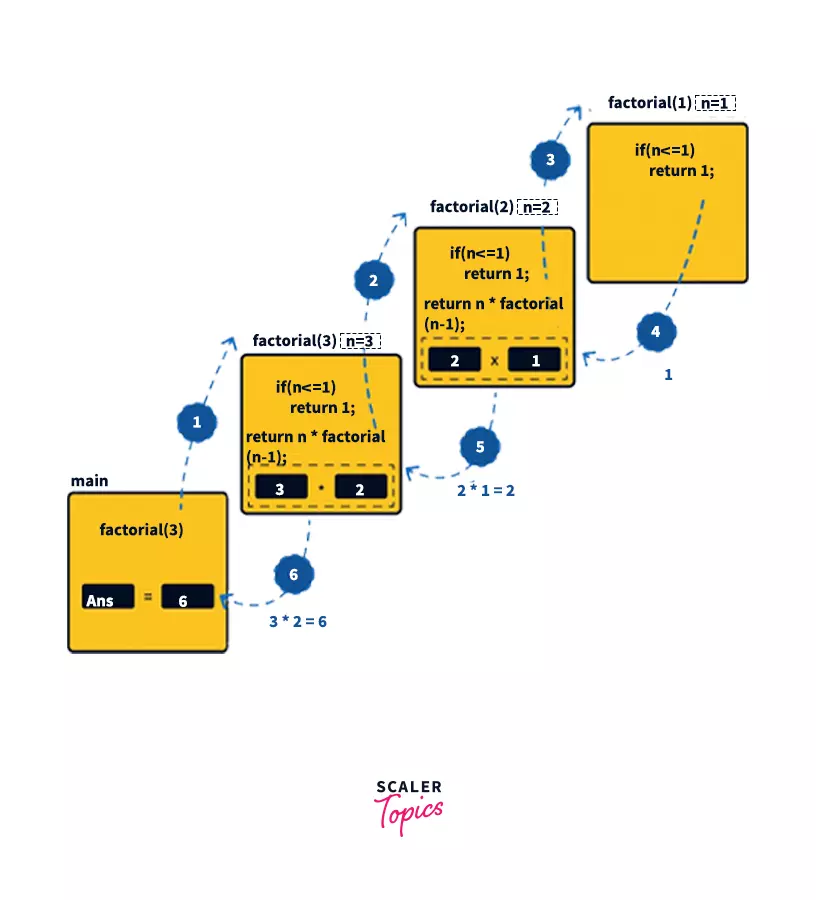
The time complexity of the above program is O(n) time. This is the case because it executes once every time it decrements the value n, and it decrements the value n until it reaches 0.

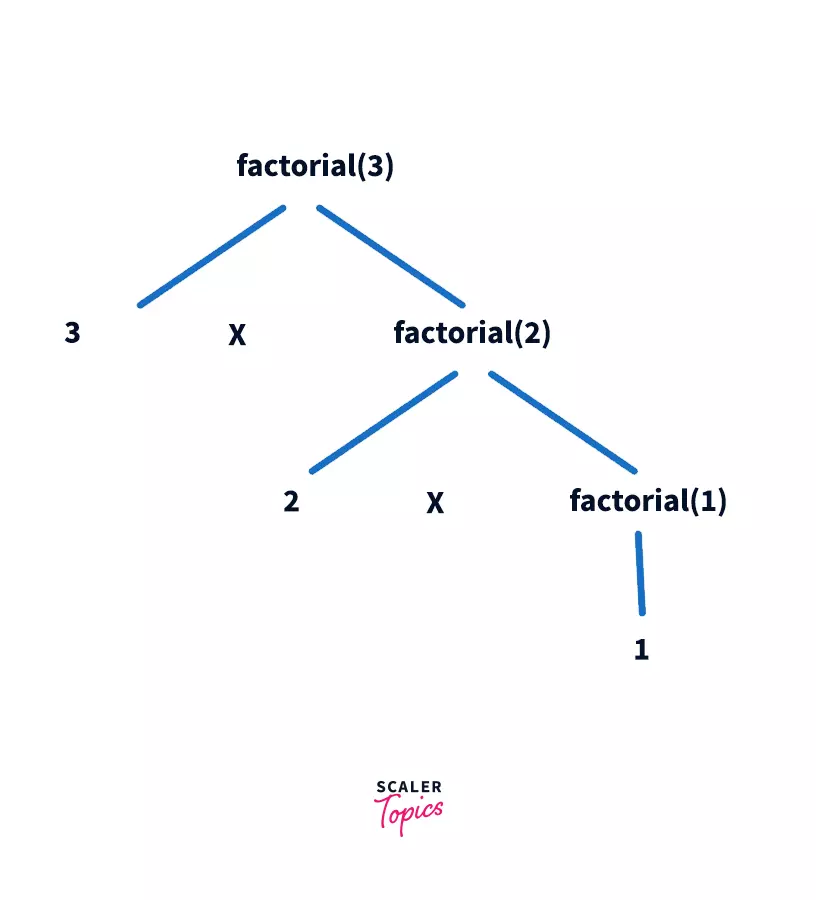
Consider the recursion tree above, the function factorial() is called 3 times because it would take three turns for the program to start from 3 and reach 0. Similarly, had we passed 5 to factorial(), the function would have been invoked 5 times. In this way, if we pass n to factorial() function, it would be called n times. Thus, the time complexity of the program is O(n). The following diagram explains the recursive calls.

Compute the factorial of a number in C using a ternary operator

An operand that has three operands is known as a Ternary Operator. It is represented with? : .

It is also known as a conditional operator. Ternary operator is a shorthand way of writing an if-else statement.

The syntax of a ternary operator is –

The above statement evaluates to value_if_true if condition is met and value_if_false otherwise.

C program to compute factorial of a number by using the ternary operator

The flow of the given program is similar to what we observed in the program to find the factorial of a number by recursion. The only difference here is, we are using a ternary operator to evaluate the condition. Though there is not much difference in using a ternary operator, we are using it since it makes our code more readable and maintainable. Furthermore, the ternary operator can only be used if there are two conditions.

Instead of writing this piece of code –

We are writing –

The above statement means that if n is equal to 0, return 1 otherwise, return n * factorial(n – 1).

The time complexity of the above program is the same as that of a recursive function that is O(n). This is the case because it executes once every time it decrements the value n , and it decrements the value n until it reaches 0. Further, the ternary operator being of constant time complexity will show no effect on the overall time complexity of the program.

Compute the factorial of a number in C using the tgamma() method

tgamma() is used under the header file <math.h>. The tgamma() function computes the gamma function of an argument passed to the function.

For a number n –

Here, n can be a floating point value and, tgamma(n) returns the gamma function of n. This method does not work for negative, 0 and infinite numbers.

For a value n, the tgamma() function returns –

+inf/-inf, for n = 0 NAN, for n = -inf +inf, for n = +inf NAN, for n = -ve NAN, for n = NAN Where NAN = Not a Number and inf = infinity

A gamma function can be expanded as follows:

We have discussed a lot about the gamma function, but why does it matter and how do we use it? Gamma function is a generalization of the factorial function to non-integral values. It was introduced by the Swiss mathematician Leonhard Euler.

Thus in C, if we consider a number n, the tgamma(n) would return n! where ! denotes factorial of n.

C program to compute factorial of a number by the gamma() method

Since now we know that the tgamma() function returns the factorial of a number, we can use it in our C program. For a number n, we should call tgamma(n + 1), this would give us the value of n!.

We are using passing n + 1 to the function because the gamma function is evaluated over a value lesser than the original value by 1. This means that calling tgamma(n) would give us the factorial of n – 1.

Now, let us understand the flow of this program –

1. Declare a variable, n in the main() function.
2. Ask the user to input the number, n to calculate its factorial. Let it be 3.
3. Set the value of n equal to tgamma(n + 1). We are passing n + 1 to the tgamma() function since the gamma function is evaluated over (n – 1). For n = 3, n = tgamma(4) = 6.
4. Print the value of n (6 in this case).

Note – the tgamma() method can only be used till 20!.