Min Heap and Max Heap
Learn via video course

Abstract
A heap is a binary tree with all levels except the last filled. Typically heap is represented using an array. The elements in a heap can be rearranged such that some operations(e.g. getting maximum or minimum element) on the heap can be made faster. These arrangement are called Min heap and Max heap. This is especially useful when the data in the heap is in the form of a stream(i.e. you keep getting new data to add to existing data).
Scope
- The article gives a brief introduction to heaps and explains Min heap and Max heap as two variations of heap.
- It explains when to use min heap and max heap.
- It shows how heap can be represented using an array.
- It discusses the time complexities for common operations on heaps.
- It does not go over the code implementation for heap operations.
- It compares Min heap and Max heap.
Takeaways
- Operations on Min and Max heap
- Get min/max Element
- Remove min/max Element
- Insert an Element
Introduction
Consider a line outside a vaccination center. The center gives vaccines according to people's age. i.e. The person who has the highest age gets the vaccine first. How do we ensure that the person at the start of the queue has the maximum age? One option would be to sort the people according to their age.
But what if a new person comes in with an age higher than everyone in the queue? Now everyone will have to push back and make a place for the new person which will take time. We need to arrange the people in such a way that getting the person with maximum age is fast and at the same time accomodating new people in the line should not take time. Max heap comes to the rescue here.
Before we go to max heap and min heap let's have a quick recap of what heap is.
Heap is a data structure that is represented using a tree where all the levels except the last are filled (such a tree is called a 'complete binary tree'). The last level of the tree should be filled from left to right.
Example of heaps: Both the trees shown below have all levels filled from left to right

Examples of Trees That are Not Heaps:
The last level is not filled from left to right(the right child of the node with value 12 is missing) hence the tree below is not a heap.

You can read more about heaps here.
What is Max Heap?
Max heap is a type of heap data structure we saw above with a special property. In a Max heap, every node's value is greater than or equal to both its children. How does this help us? If every parent is greater than its children, which node would have the greatest value? That's right - the root node. You can directly access the root node to get the maximum element in a max heap.
More formally:
For a tree to be a max heap it should follow both these conditions:
- The tree should be a complete binary tree (this is the condition for heap)
- Value of each node must be greater than all its children
In the following example of the max heap, notice every node is greater than both its children.
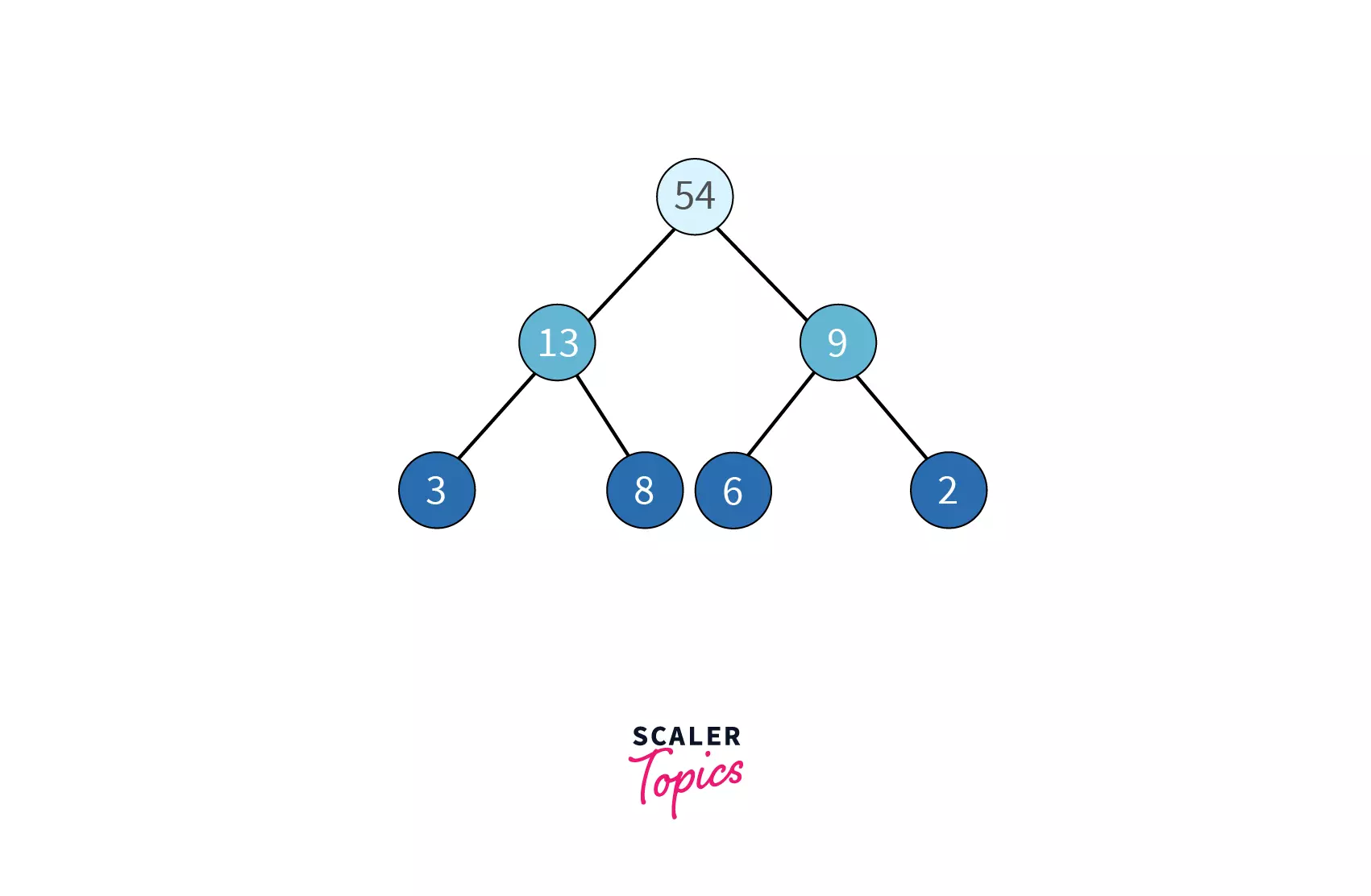
Coming back to the problem we saw at the start of the article. If we arrange the people in form of a Max heap, the person at the root will always have the maximum age.
What is Min Heap?
Similar to the Max heap, the Min heap is also a type of heap but the condition for a min heap is almost reverse. In a min heap, every node's value is smaller than or equal to both its children.
More formally:
For a tree to be a max heap it should follow both these conditions:
- The tree should be a complete binary tree (this is the condition for heap).
- Value of each node must be smaller than all its children.
This means that the root of the tree will be the node with a minimum value.
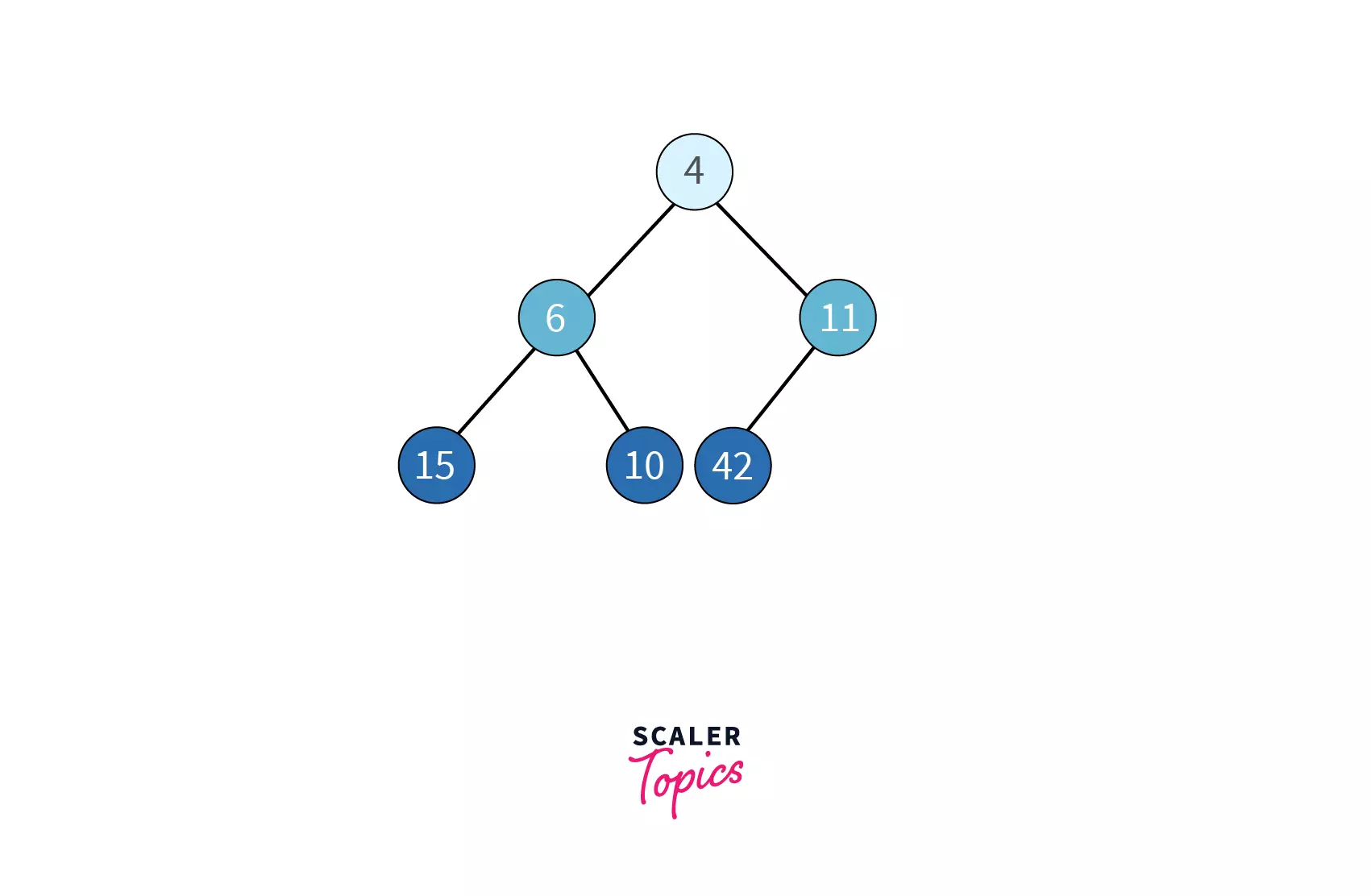
In the following example of the min heap, notice every node is smaller than both its children.
 )
)
When to Use a Min Heap vs When to Use a Max Heap?
Let's say you want to build a job scheduler. Jobs keep coming in randomly each taking different times to complete. The job scheduler should be such that every time the Operating System(OS) asks for a job, it should give the 'job that takes the least time'. You can store the elements in an array and scan the array every time the OS needs an element to find the min and provide it to the OS. This will(in the worst case) take O(n) time to pick every job, where N is the current number of jobs. Instead, if we use a min-heap, it will get us the minimum element in O(1) every time.
NOTE:
Once we get the first minimum we need to reorder the min-heap before we do the next query. The operation takes O(log(N). We will discuss this in more detail later in the article)
In contrast, consider this situation. ICC(International Cricket Council) wants to feature the cricketer with the highest score among all the retired cricketers from test cricket on their website. Here we can maintain a Max heap. Every time a cricketer retires, his/her score will be added to the Max heap. The cricketer at the root node will always have the maximum and will be featured on the ICC website.
NOTE:
Similar to Min heap we need to reorder to maintain the max-heap property after removing the max element.
There are other ways to achieve both these problems. We have used Min heap and Max heap to provide you with a sense of possible use-cases.
How are Min and Max Heap Represented?
You might think that since heap is a tree, it should be represented using a node with data and two pointers for its children. We can represent heap like that but remember heap is a special tree called a complete binary tree. This allows us to avoid all the complexity of dealing with nodes and their pointers by using a simple array to represent the heap. Let us see how it is actually represented with a simple example. Consider the heap below:

This heap can be represented using the array: [0,1,2,3,4,5,6]. To keep things simple, we have kept the array index equal to the value. Notice that for every node we can find its children and parent using the following formulae:
For a node at index i:
- Left child node index = 2*i + 1
- Right child node index = 2*i + 2
- Parent node index = i/2
The below illustration shows how the formula is applied at each node

As we saw before a heap is really a binary tree. We can use this same representation for any complete binary tree.
NOTE:
Similar to a regular tree, heaps can be represented using an adjacency matrix or adjacency list. But that would add an unnecessary layer of complexity. The binary property of most heaps allows us to use the simple yet elegant array representation.
Operations on Min and Max heap
1. Get min/max Element
Whenever our requirement is getting the minimum element, we use the Min Heap. When we want to get the maximum element we use the Max Heap. By the definition of min heap, all the parent nodes should be less than the child nodes. This implies that the great (great great...) grandparent i.e. the root of the tree should have the element with the least value in the complete tree.
Getting the root of the tree is a constant time operation. Hence the time complexity would be O(1).
Similarly getting the maximum element will be at the root of the max heap, taking O(1) complexity.
NOTE:
Getting minimum element from Max heap or maximum element from Min heap is not constant time operation.
But what if now we want the next largest element? Every time you delete the root element from the heap, you need to rearrange the tree so that it satisfies the max heap property. Lets see how to do that in the next section.
2. Remove min/max Element
Steps to remove the min element from Min-heap:
- Swap the root with the last element in the array.
- Decrease the array size by one.
- Starting from the root, at every node swap the current node with the smaller child node.
- Keep repeating step 3 until both children are greater than the parent or both children are null.
Let us walk through them with an example. Consider the following initial state of the min heap. We want to remove the minimum element i.e. 4 from the root.

-
Swap 42 and 4

-
Delete 4 by reducing the size of the array by one.

-
Starting for 42, out of 6 and 11, 6 is the smaller child. So we swap 42 and 6.

-
In our example after the first swap, 42 is greater than both its children so we can stop the algorithm.
Steps 1 and 2 above are constant-time operations. Steps 3 and 4 traverses the complete depth of the tree in the worst case, hence the time complexity would be equal to the depth of the binary tree i.e. O(log(N)).
Similar logic can be followed for Max Heap except that in step 3 we will swap the current node with the greater child and we repeat the process till both children are smaller than root or are null
3. Insert an Element
Steps for inserting into a Min-heap:
We will follow there with the example
-
Insert the new incoming element at the only available position (i.e. end of the array)
-
At every node we ask the question: Is the inserted node less than the parent? - If the answer is yes: Swap the inserted node and parent. - else return the array
Let us walk through them with an example. Consider the following initial state of the min heap. We want to add 1 to the min heap.
 1. Add 1 to the end of the array
1. Add 1 to the end of the array  2. The parent of 1 i.e. 11 is greater than 1 so we swap them. The new parent of 1 is 4 which is greater again so we swap them too. 1 does not have a parent now so we stop the algorithm
2. The parent of 1 i.e. 11 is greater than 1 so we swap them. The new parent of 1 is 4 which is greater again so we swap them too. 1 does not have a parent now so we stop the algorithm
For the first step, adding an element at end of the array is a constant time operation i.e. O(1). For the 2nd step, in the worst case, you will have to traverse the tree from the leaf up to the root. i.e. Traversing the complete height of the tree in the worst case. This will take O(log(N)) time.
The same logic can be applied to insert into a max heap. Only change being - at step 2 we will ask the question: 'Is the inserted node greater than the parent?'
Min Heap vs Max Heap
| Min Heap | Max Heap |
|---|---|
| Every node is less than all its children | Every node is greater than all its children |
| Minimum element in the complete tree is at the root of the tree and can be retrieved in constant time | Maximum element in the complete tree is at the root of the tree and can be retrieved in constant time |
| It is a complete binary tree represented using an array | It is a complete binary tree represented using an array |
Example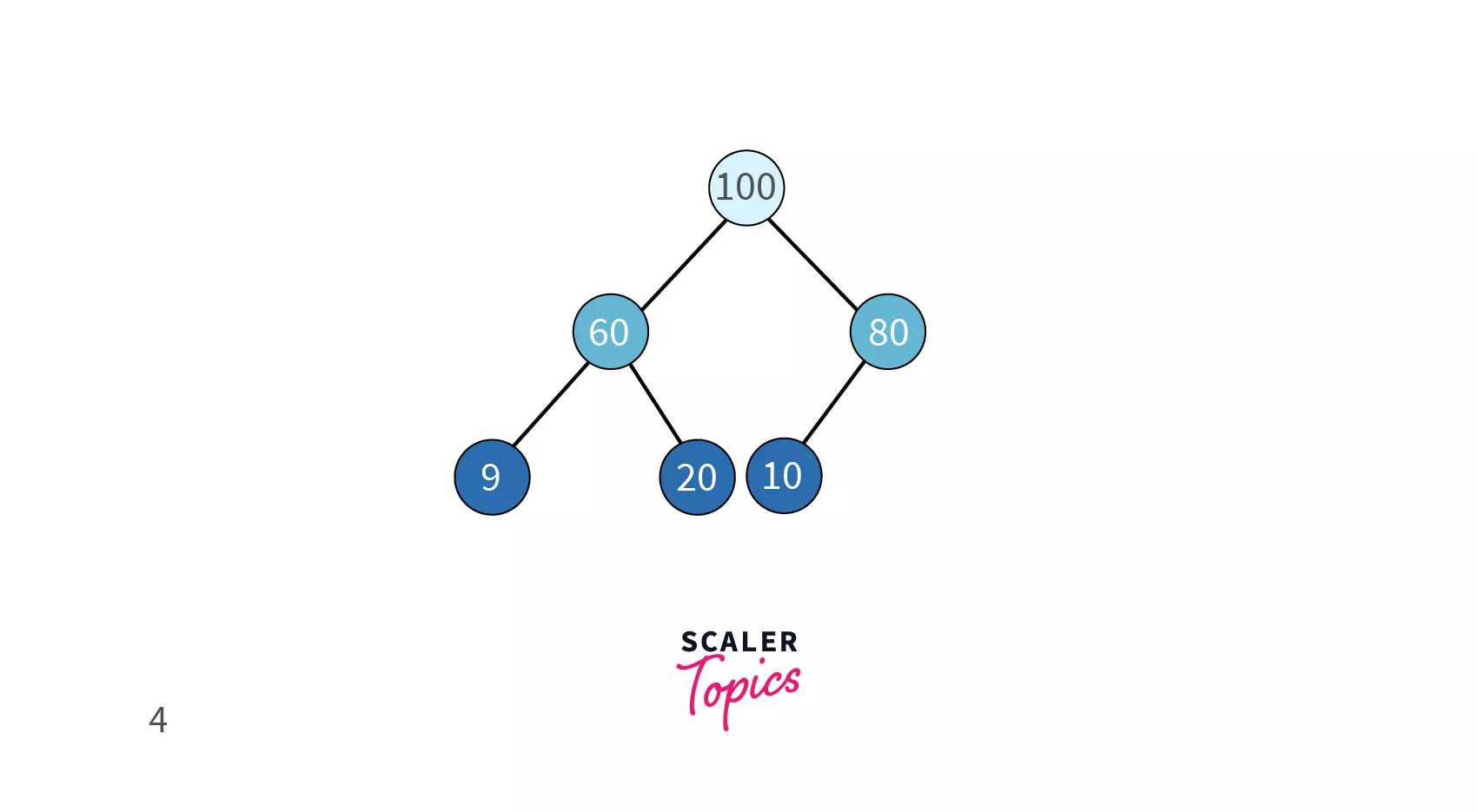 | Example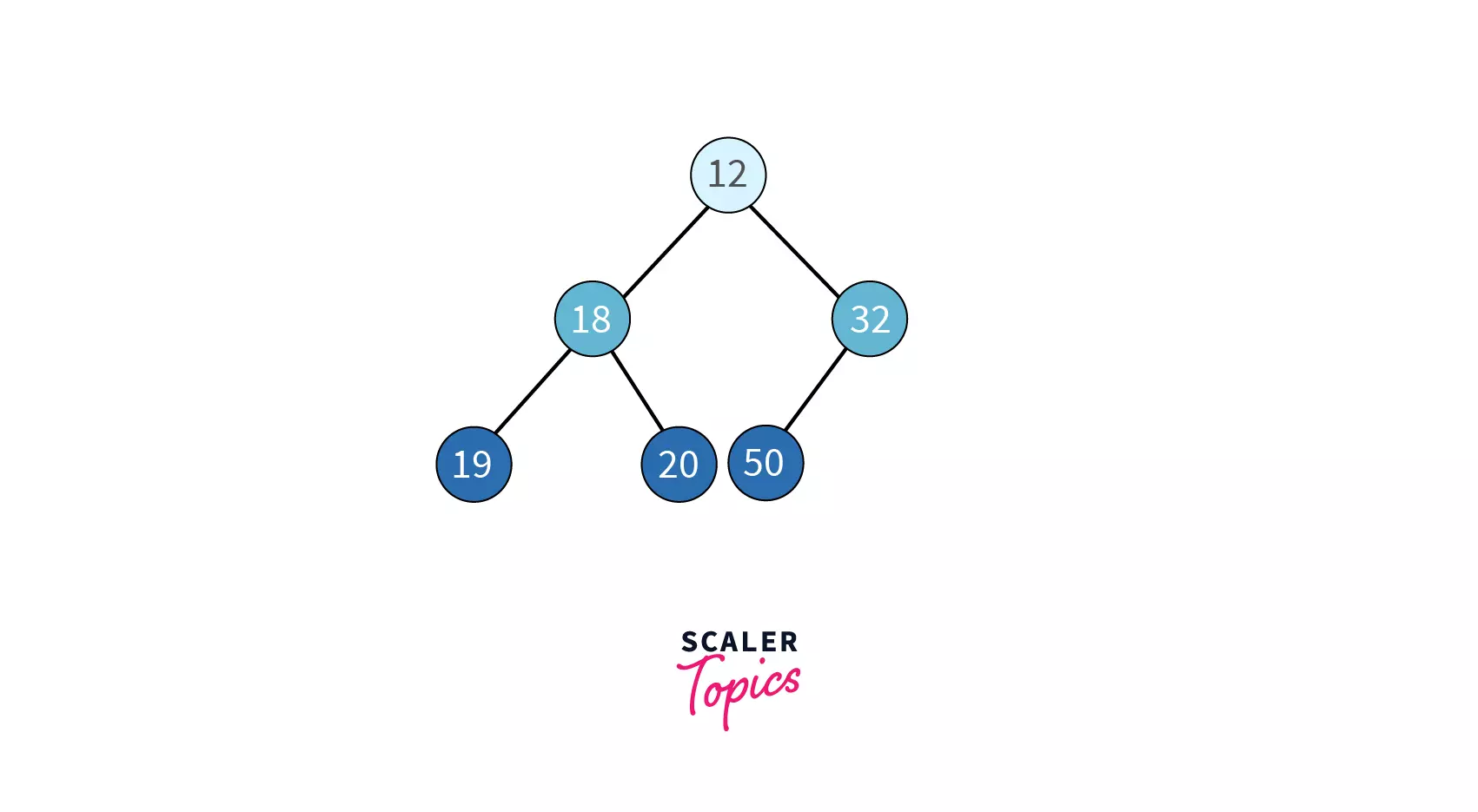 |
Conclusion
In this article we saw:
- Min heap and max heap are complete binary trees.
- Both min heap and max heap can be represented using an array.
- Time complexity for common heap operations for a heap with N elements:
- Getting the minimum element from min heap or maximum element from max heap: O(1)
- Removing the minimum element from min heap or maximum element from max heap: O(log(N))
- Inserting an element in min/max heap: O(log(N))
- Min Heap data structure is useful when you need to get the minimum element in a collection of elements in constant time. Max heap is the opposite of Min Heap. Max Heap gets the maximum element from a collection in constant time.
