Different Types of Graphs in Data Structure

Graphs in data structure can be of various types and be used based on the requirements of the application.

Finite Graph

As the name suggests, a finite graph is one which has a finite (countable) number of vertices and edges, i.e. If a graph G=(V,E) consists of a finite number of vertices and edges denoted by V and E respectively, then the graph is a finite graph.

Infinite Graph

As the name suggests, contrary to a finite graph, an infinite graph is one which has infinite number of vertices and edges, i.e. If a graph G=(V,E) consists of an uncountable number of vertices or edges denoted by V and E respectively, then the graph is an infinite graph.

Trivial Graph

A finite graph G=(V,E) is said to be trivial if it has only one vertex. Since such a graph has only one vertex, it does not have any edges.

Simple Graph

A simple graph G=(V,E) is one which a pair of vertices V1 and V2 are connected by only one edge. A minimum cost graph mentioning the least cost of travelling by car between 2 places on its edges is an example of a simple graph. In such a graph, since least cost is a single value, there will be only one edge connecting 2 locations.

Multi Graph

A graph G=(V,E) which contains more than 1 edge or a loop (not self-loop) between 2 vertices is called a multi graph. A map of a place showing connections between places is an example of a multi graph. In such a graph, we can find more than one routes (edges) connecting 2 places (vertices), some of which could be longer, others shorter.

Null Graph

A null graph G=(V,E) is one which has only isolated vertices, ie. such a graph does not have any edges connecting the vertices. An example of such a graph would be importing an item from a foreign country to your place when there is no transport connecting the places.

If we consider the 2 locations to be vertices, then due to no route between them, there would be no edges connecting them.

Complete Graph

A graph G=(V,E) is said to be complete if each vertex in the graph is adjacent to all of its vertices, i.e. there is an edge connecting any pair of vertices in the graph.

An undirected complete graph with n vertices will have n(n-1)/2 edges, while a directed complete graph with n vertices will have n(n-1) edges. The following figure shows graphs Ki where i represents the number of vertices.

We can clearly see how all the vertices in each graph have an edge connecting each other.

Pseudo Graph

A pseudo graph G=(V,E) is a graph that contains self loop and multiple edges. Consider the folllowing pseudo graph abcd. Between a and b, there exist 2 paths. b also contains a self loop. Thus, we can say that abcd is a pseudo graph.

Regular Graph

A graph G=(V,E) is said to be regular if every vertex V of the graph is adjacent or connected to the same number of vertices. All complete graphs are regular but it isn't the same vice versa. Consider the following example.

In a 2-regular graph, every vertex is adjacent to 2 vertices, whereas in a 3-regular, every vertex is adjacent to 3 other vertices and so on.

Bipartite Graph

A graph G=(V,E) is called a bipartite graph if its vertex set can be partitioned into two non-empty disjoint subsets A and B such that every edge (a,b) connects a vertex from A to B or vice versa. In bipartite graphs, there would be no edge that connects vertices from the same set.

A bipartite graph can be represented by colouring vertices of the different subsets in different colours. As shown in the below example, the vertices of the figure shown that can be split into 2 sets are depicted in blue and purple respectively.

Further they are added to their respective set and the connections can be shown in the image to the right.

Labelled Graph

A labelled graph G=(V,E) is one in which the vertices and edges of a graph are labelled with a name, data, or weight. This type of graph is also known as a weighted graph since the edges can consider some useful information.

These graphs are very useful in various purposes like calculating the minimum distance or shortest path between 2 places.

Digraph Graph

A digraph, also known as a directed graph, is one in which the vertices are ordered in a particular sequence. Thus, the edges are usually represented by arrows that point in a particular direction.

In such a graph, changing the direction of arrows can alter the meaning of the graph. In the following figure A points to B, B to C, C to E, E to D, D to B and E to F.

Digraphs are commonly used in marking hierarchies in network administration, social media connection graphs and roadways.

Subgraph

A graph in data structure is said to be a subgraph if it is a part of another graph. In the following example, graphs H1, H2 and H3 are subgraphs of the graph G.

2 Types of Subgraph

Vertex Disjoint Subgraph

A subgraph with no common vertex is called a vertex disjoint subgraph. Any two graphs A = (V1, E1) and B = (V2, E2) are said to be vertex disjoint of a graph G = (V, E) if V1(A) intersection V2(B) = null.

Since vertices in a vertex disjoint graph cannot have a common edge, a vertex disjoint subgraph will always be an edge disjoint subgraph. In the above example, since subgraph EFG and ABCD have no vertex in common, they are said to be vertex disjoint subgraphs.

Edge Disjoint Subgraph

A subgraph with no common edge is called an edge disjoint subgraph. A subgraph is said to be edge disjoint if E1(A) intersection E2(B) = null. In the above example, since graphs ABCD and BEFG have no edge in common, they are said to be edge disjoint subgraphs.

Connected or Disconnected Graph

A unidirected graph is connected if there is a path from any vertex to any other vertex, or any vertex is reachable from any other vertex. A connected graph of n vertices has at least n-1 edges.

A disconnected graph is one that is not connected, i.e. at least one of the vertices is not connected to any other vertex.

Cyclic Graph

A graph that has one or more cycles is called a cyclic graph. A jogging path around the city that connects various landmarks could be considered as a cyclic graph. In the following figure, BCDE represents a cyclic graph since it consists a cycle denoted by BCED.

Vertex Labeled Graph

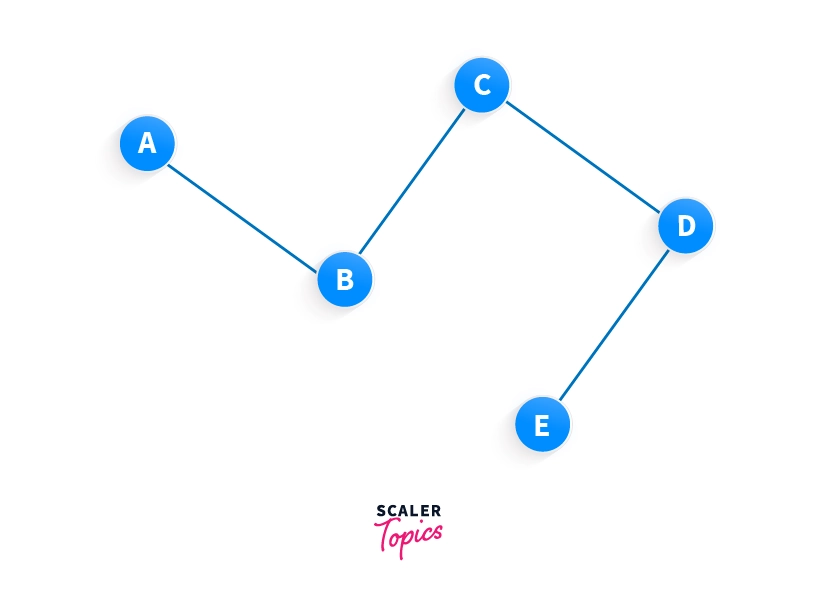
A vertex labeled graph is one that holds some data in its vertices, in a way that they determine data of the edges. Consider a pair of vertices A and B, the edge between them can be thus called AB based on the label of the vertices. Such graphs are most useful in a road map where the label of vertices can be considered as the names of the landmarks. In the following figure, A, B, C, D, E represent the labels of a vertex labeled graph.

Directed Acyclic Graph

A directed acyclic graph, commonly known as DAG is a directed graph that doesn't contain any cycles. DAGs may be used to represent data flows, network of processing elements and even in project management.

Since in the following figure, the edges represent directions and there is no cycle present, the given graph is a DAG.