Stack in Data Structure

Introduction

Imagine this. You want to buy the latest edition of your favorite laptop from your nearby mall. You reach the mall and spot an elevator to reach the destination. But, uh oh, the elevator is crowded, and there is no more space. You still, however, make it and enter the elevator.

Now when the elevator reaches the destination floor, who would be the first one to get out? Undeniably, you! since you were the last one to get in that crowded elevator and there was no other way out.

Let us now consider the event where you luckily found the lift empty and boarded it first, but it soon got crowded. At what position will you leave the elevator now? Most probably, at last, since you were the first one to enter.

In the above-given example, there are two main points on which we want you to focus-

1. The person who entered, at last, was the first one to leave the elevator.
2. The person who entered first was the last one to leave the elevator. By now, you must be wondering why this is even significant. Short answer – because this is precisely how a stack in data structure works.

Let us now gear ourselves up to dive deeper and understand what a stack is and why it matters.

In this article, the following will be the flow of our discussion –

1. What is stack in data structure?
2. Features of stack data structure
3. Stack operations
4. How is stack data structure implemented?
5. What are the applications of stack in data structure?

What is Stack in Data Structures?

By definition, a stack is an ordered list in which insertion and deletion are done at one end, where the end is generally called the top. The last inserted element is available first and is the first one to be deleted. Hence, it is known as Last In, First Out (LIFO) or First In, Last Out (FILO). In a stack, the element at the top is known as the top element.

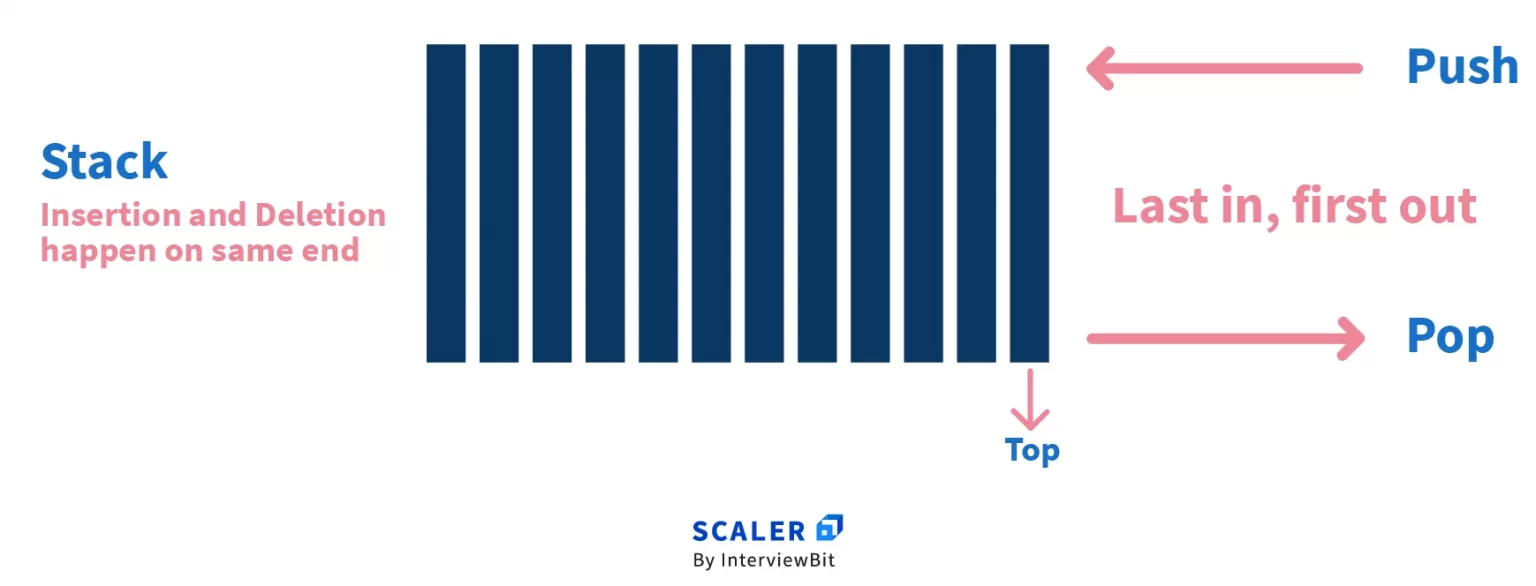
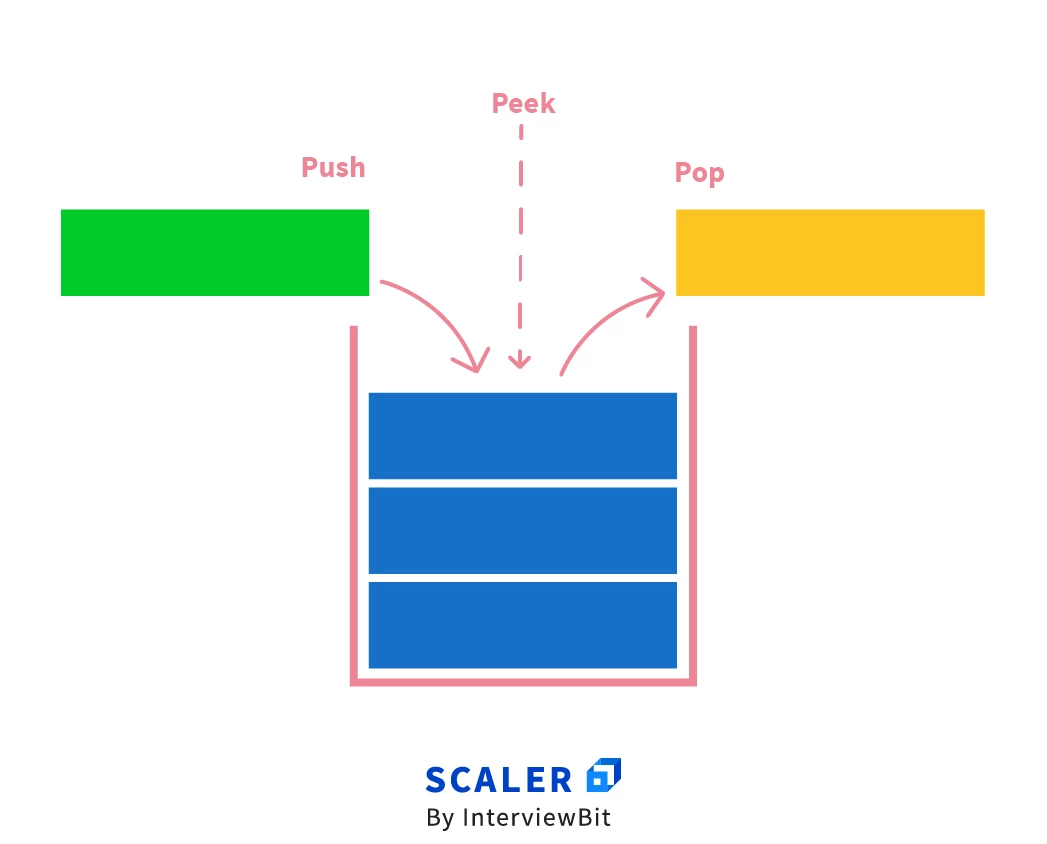
The operations of inserting and deleting the elements in a stack are called push() and pop() respectively.

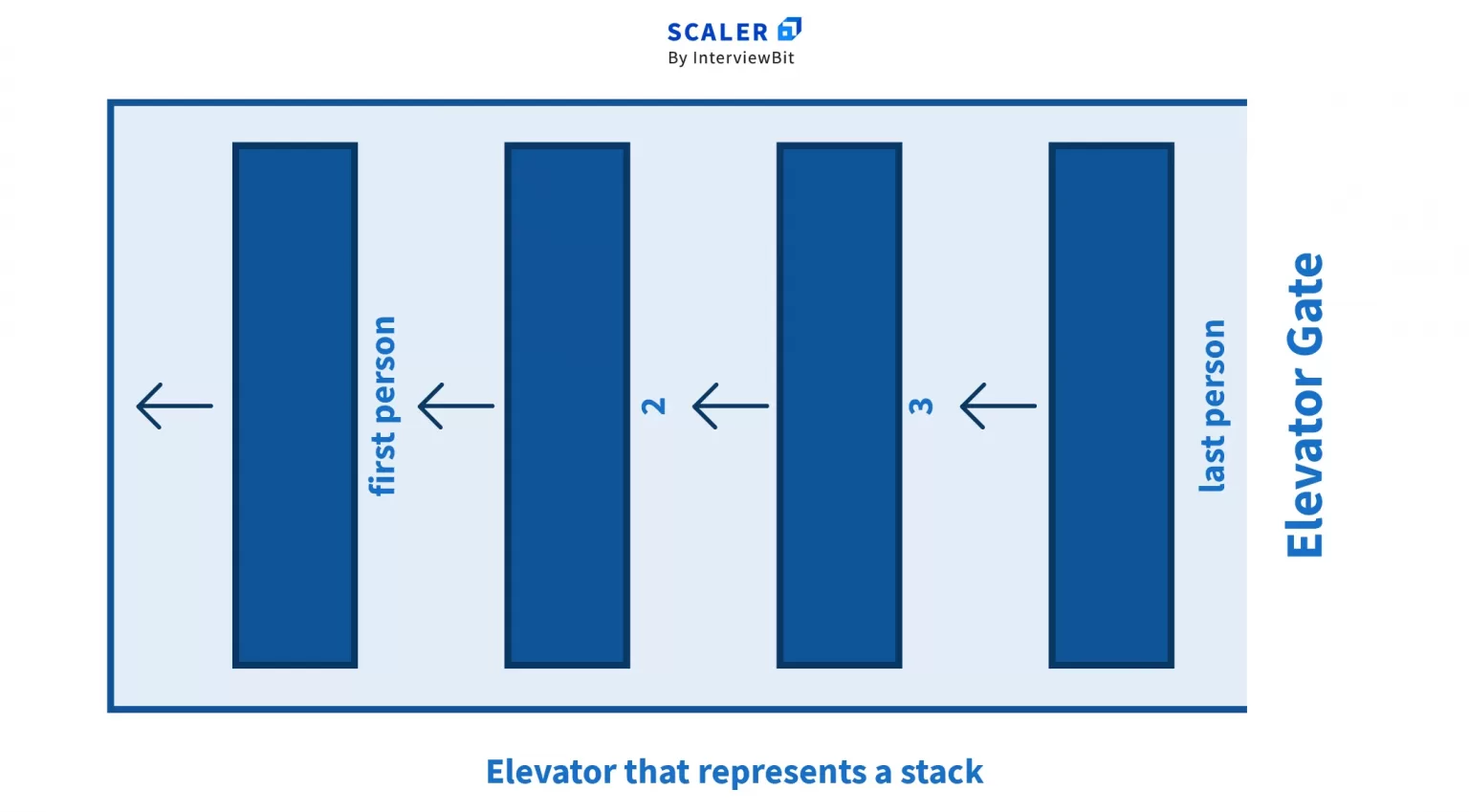
Recall the above example of the crowded elevator. In that case –

1. The elevator represents a stack
2. The people represent the elements inside the stack
3. The elevator gates represent the entry point in the stack that is the only point from where insertion or deletion can be done
4. And, the person who gets in the elevator at the last would be the first one to get out. This represents the Last In First Out (LIFO) nature of the stack

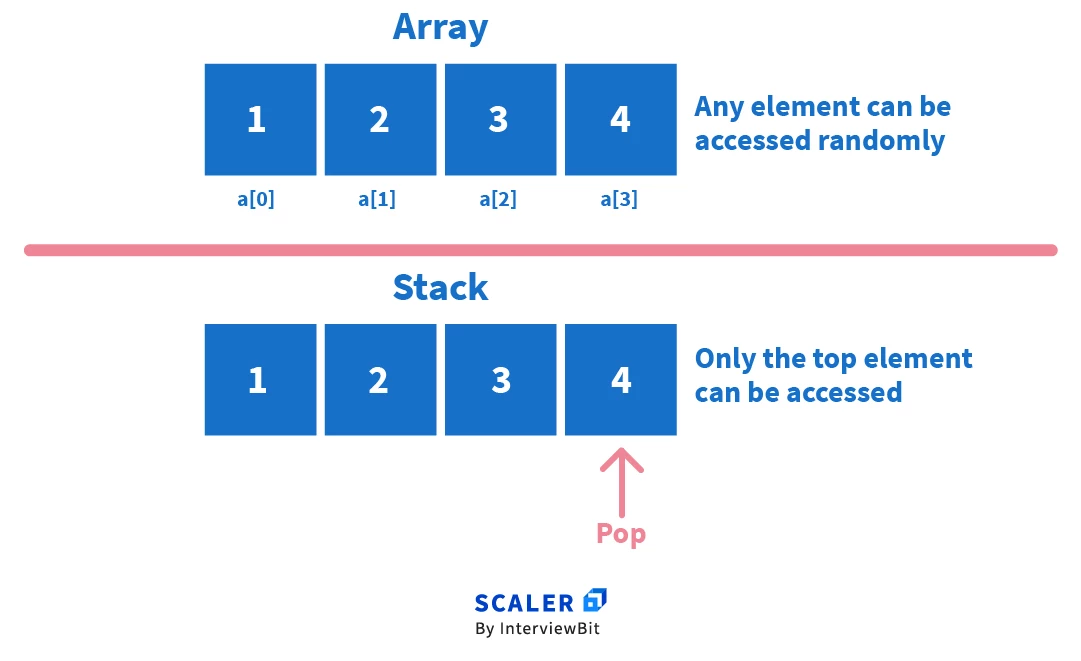
Just like arrays and linked lists, a stack is a linear data structure that is used for storing data. One thought that arises here is, “what is the difference between arrays and stacks?” or “what is the difference between linked lists and stacks?”.

Stacks differ from the arrays in a way that in arrays random access is possible; this means that we can access any element just by using its index in the array. Whereas, in a stack only limited access is possible and only the top element is directly available.

Consider an array, arr = [1, 2, 3, 4]. To access 2, we can simply write arr[1], where 1 is the index of the array element, 2. But if the same is implemented using a stack, we can only access the topmost element which is 4.

Coming to linked lists the data can be accessed from any end, while this is not possible in a stack. In other words, linked lists allow us to access any middle element without removing the first or last elements, while in stacks, to access any middle element we should remove all the elements above it.

We can use both arrays and linked lists to form a stack. We will be doing this super soon!

Features of Stack in Data Structure

• Stacks are dynamic in nature; this means that they do not have a fixed size and their size can be increased or decreased depending upon the number of elements.
• In stacks, only one end is available to perform actions like insertion or deletion of the elements
• Stacks follow LIFO, which is Last In, First Out mechanism. Inserting an element is known as push, and deleting an element is known as pop

Stack Operations in Data Structure

There are some main and auxiliary actions that can be performed over a stack. Some of them are listed below. The time complexity of all the given operations is constant, that is O(1).

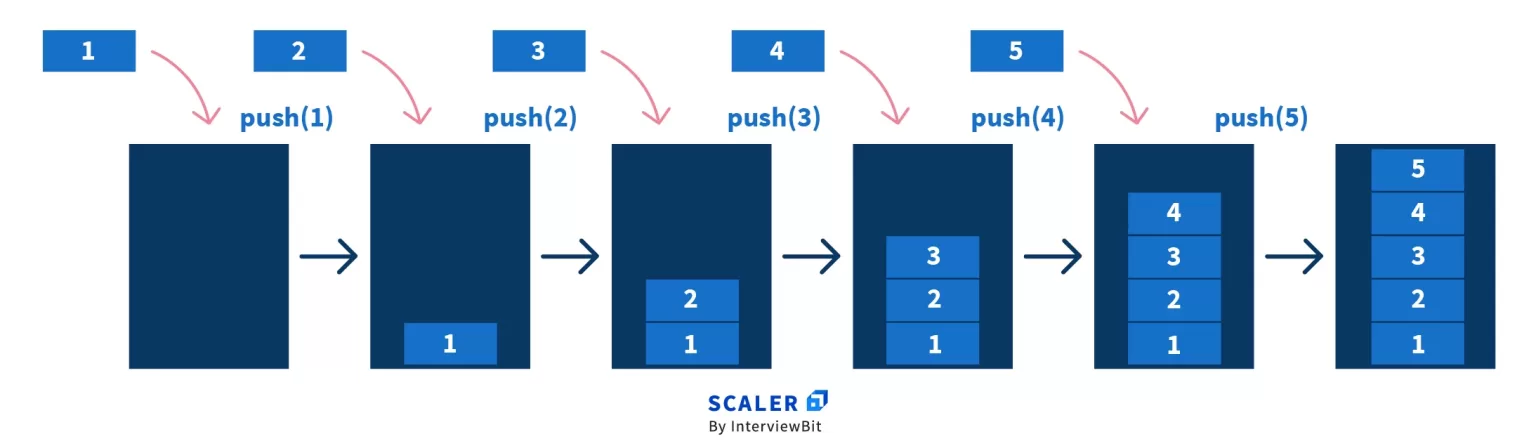
1. push(x)

The process of inserting new data into a stack is known as push. The push (x) operation takes the element to be added as a parameter

If we are implementing a stack using an array, it may have a pre-defined capacity , which means that only a specific number of elements can be stored in it. In this case, if the stack is full, it results in a condition called stack overflow. It indicates that we have utilized the entire capacity of the given stack, and there is no space for any new element.

The steps involved in a push operation are –

1. Before inserting the element, check whether the stack is full.
2. If the stack is full, print “stack overflow” and terminate the program.
3. If the stack is not full, add data into the stack.
4. We can repeat the above steps until the maximum capacity of the stack is achieved.
   Recall the above example of the elevator, the event of people walking into the elevator closely relates to pushing the elements into a stack.

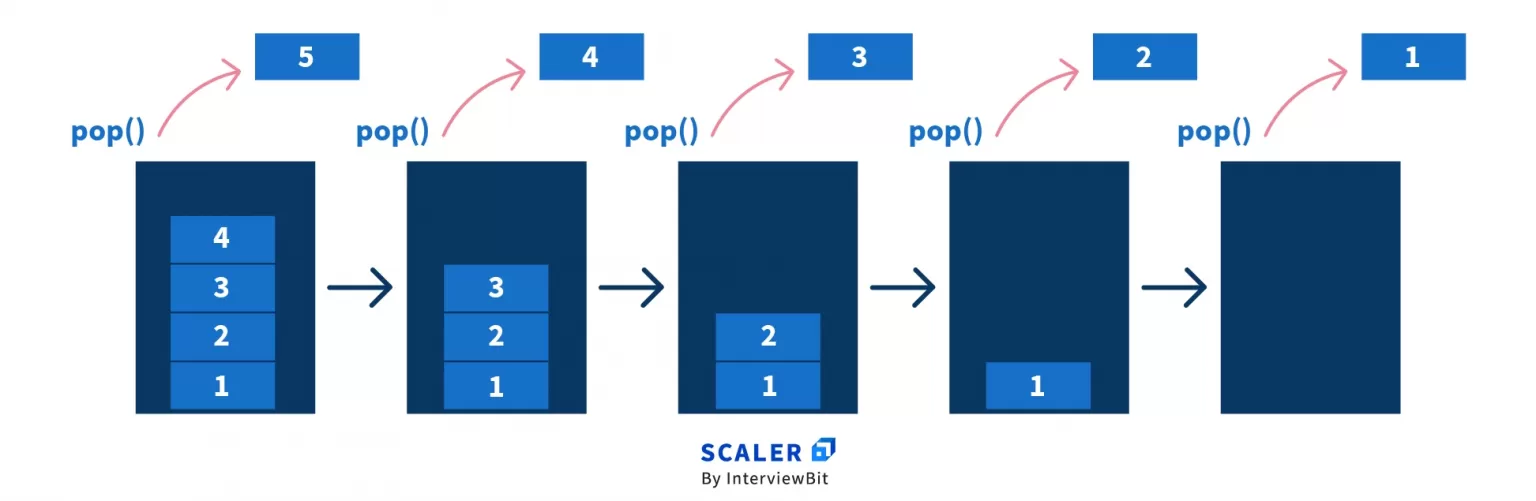
2. pop()

The process of deleting the topmost element from the stack is known as pop.

In stacks, if we try to pop or remove elements if the stack is empty, it results in a condition known as underflow. It means that there is no element in the stack that can be removed.

The steps involved in a pop operation are –

1. Before removing the topmost element, check whether the stack is empty
2. If the stack is empty, print “Stack underflow” and terminate the program
3. If the stack is not empty, access the topmost element and let the top point to the element just before it
4. We can repeat the above until all the elements from the stack are removed

In the example of the elevator, a person moving out from it resembles what we call a pop operation.

3. topElement()/peek()

This operation on a stack returns the topmost element in a stack. This operation is also known as the peek() operation on the stack.

4. isEmpty()

This operation is used to check if the given stack is empty. It returns a boolean value; that is true when the stack is empty, otherwise false.

5. isFull()

This operation is used to check if the given stack is full. It returns a boolean value; that is true when the stack is full, otherwise false.

6. size()

This operation determines the current size of the stack

Implementation of Stack in Data Structure

There are many ways to implement a stack, however, two of the major ways in which a stack can be implemented are –

1. Using a one-dimensional array
2. Using a single linked list

1. Implementation of Stacks Using a One-dimensional Array

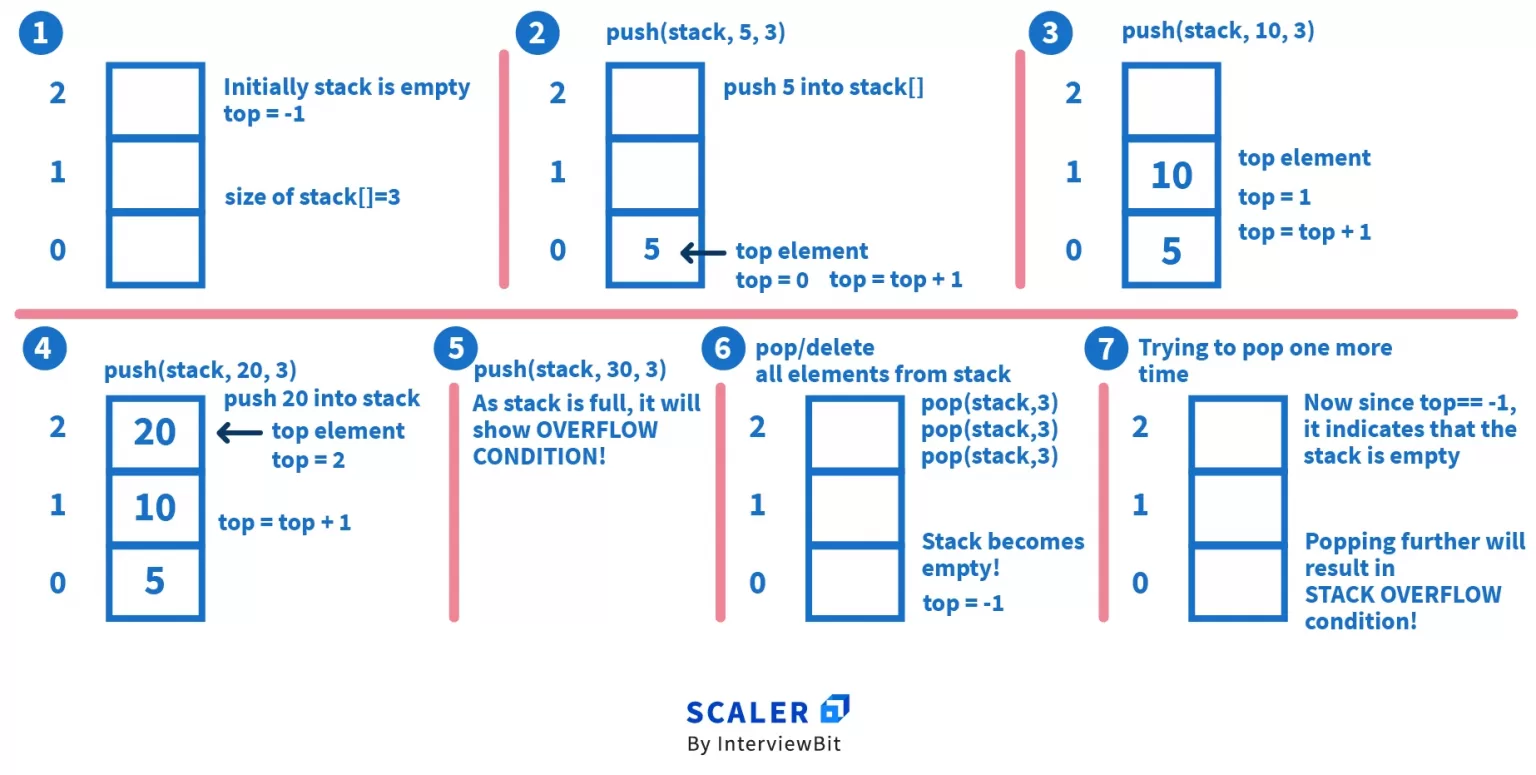
Let us understand how the array implementation of the stack works through the following steps –

1. A variable called top is used to keep track of the top element in the stack
2. When initializing the stack, we set the value of top equal to -1 so that we can check if the stack is full or empty using its value
3. Declare a function push() that takes an array called stack[], the size of the array called n, and the element to be inserted called x as its parameters. Under the function –
   • Check if the stack is already full. If it is full, return from the function
   • If the stack is not full, increase the value of top and place the new element in the position pointed to by top
4. Declare a function called pop() that removes the top element from the stack. Under the function –
   • Check if the stack is empty. If it is, return from the function
   • If the stack is not empty, return the element at the top index in the array stack[] and reduce the value of top Note – we are not deleting the value at top index during pop() because once the pointer is moved to point to the previous element, it does not matter whatever is contained in that memory location.
5. Declare a function called topElement() that returns the element at the top index from the array stack[]
6. Declare a function size() that returns the occupied size of the array stack[]. It returns top + 1.
7. Declare a function isEmpty() that checks if top is equal to -1. If it is, it returns true, otherwise false
8. Declare a function isFull() that checks if the top is equal to the maximum size of the array stack[]. If it is, it returns true, otherwise false

Output –

The following diagrams explains the flow of the code –

Limitations of Implementing Stacks Using an Array

1. The maximum size of the array must be defined in advance
2. The size of the array cannot be changed during the implementation

2. Implementation of Stacks Using a Single Linked-list

To implement a stack, we can also use a linked list. Linked lists help in allocating the memory dynamically.

The time complexity of all the operations in both implementations is the same, that is O(1).

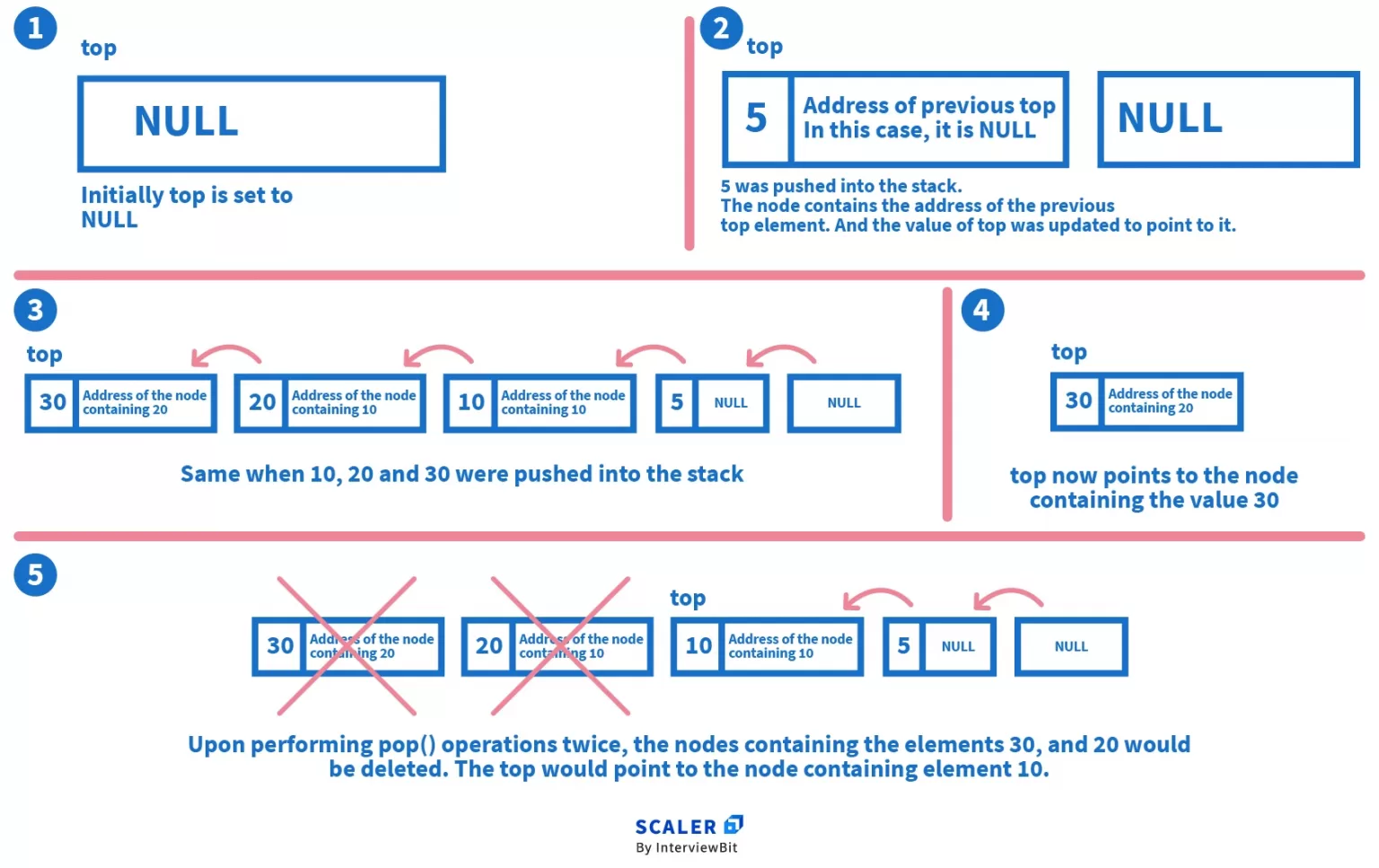
In linked list implementation of stack data structure, the nodes are non-contiguously maintained in the memory and each node contains the address of its immediate successor node.

If the space left in the memory heap is not enough to create a new node, it is known as the overflow condition.

Let us understand how the linked list implementation of the stack works through the following steps –

1. We create a class or structure Node with instance variables, data, and next. data will contain the element to be inserted and next will contain the address of the previous element in the linked list
2. To keep track of the topmost element, create an instance of the class Node called top
3. Declare a function push() that takes data as a parameter and adds it into the existing linked list. Under the function –
   1. A temporary instance of the class Node is created, and memory is allocated for the same.
   2. Check if the heap is full. If it is, print “Stack Overflow”
   3. If the heap is not full, add the data into the temporary instance
   4. Store the address of the previous top in the address part of the temporary instance
   5. Update the top so that it points to the temporary instance that contains the newly inserted value
4. Declare a function pop() that deletes the current top, and point it to the element just before it. Under the function –
   1. Check if the stack is empty or not. If it is, print “Stack Underflow”
   2. If the stack is not empty, make the top point to the previous element
   3. Free the memory which was used by the element that was popped

Output:

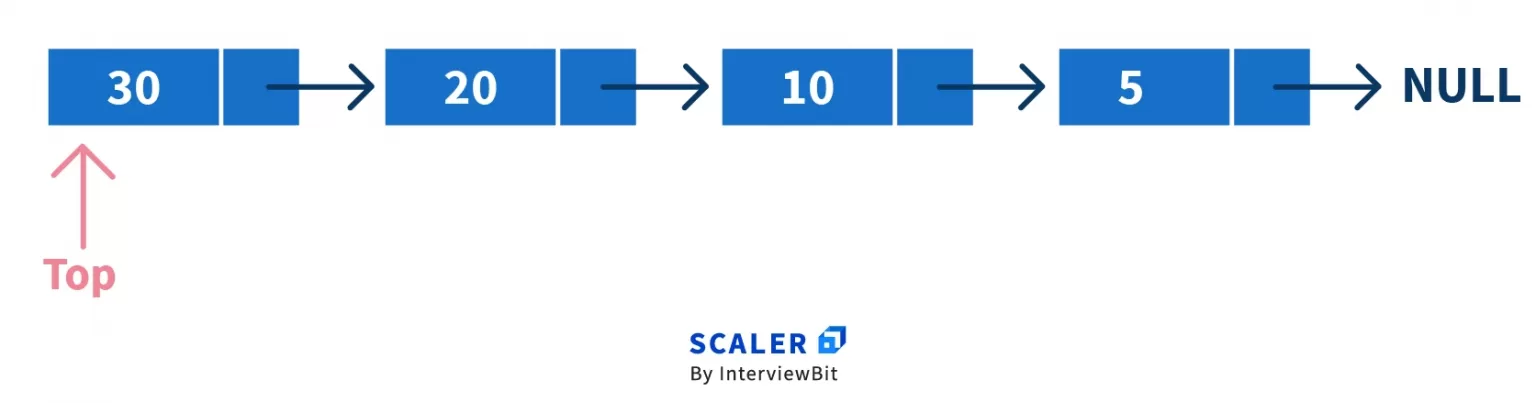
To better understand the above program, consider the above-given diagram. This diagram shows how the nodes are linked in a stack.

Applications of Stack in Data Structure

1. In code editors – Stacks are used in various code editors like VS Code, Atom, etc. to match the opening and closing tags in the languages like HTML, XML, etc.

2. In matching bracket pairs – This is one of the most famous applications of stacks. Stacks help us in identifying if the bracket pairs in a sentence or string are complete or missing.

3. In browsers – You are reading this article in your web browser, what will happen if you press the back button present at the left-hand corner of your screen? It would take you back to your last visited website or link. It is done using stacks. Every time you visit a new link, it is stored in the stack. And, every time you press the back button, the current link is popped out from the stack, and the previous link is made available.

4. In compilers – Stacks are used heavily by the browsers to convert infix expressions to postfix expressions. It is done because the compilers can not read an expression directly. E.g., if there is an expression – 5 + (1 + 4/2), the compiler cannot process it like humans. Thus, it solves this expression by converting it into a postfix or prefix expression