Red Black Tree

Introduction to Red Black Tree

In binary search trees, we have seen that in the worst case we have seen that the overall shape of the binary tree depends on the order of insertion, and deletion and hence it is difficult to maintain logarithmic time complexity. To obviate that difficulty, in this article we will discuss the notion of "RED BLACK Trees"

Red-black trees are self-balancing binary search trees where each node has one extra attribute which denotes its color (either RED or BLACK). Nodes are colored to ensure that the height of the tree remains balanced after insertion or deletion from it. It is developed by Rudolf Bayer in 1972.

We are assigning a color to each of the nodes in a red-black tree to maintain its height during the insertion and deletion operation of nodes in it.

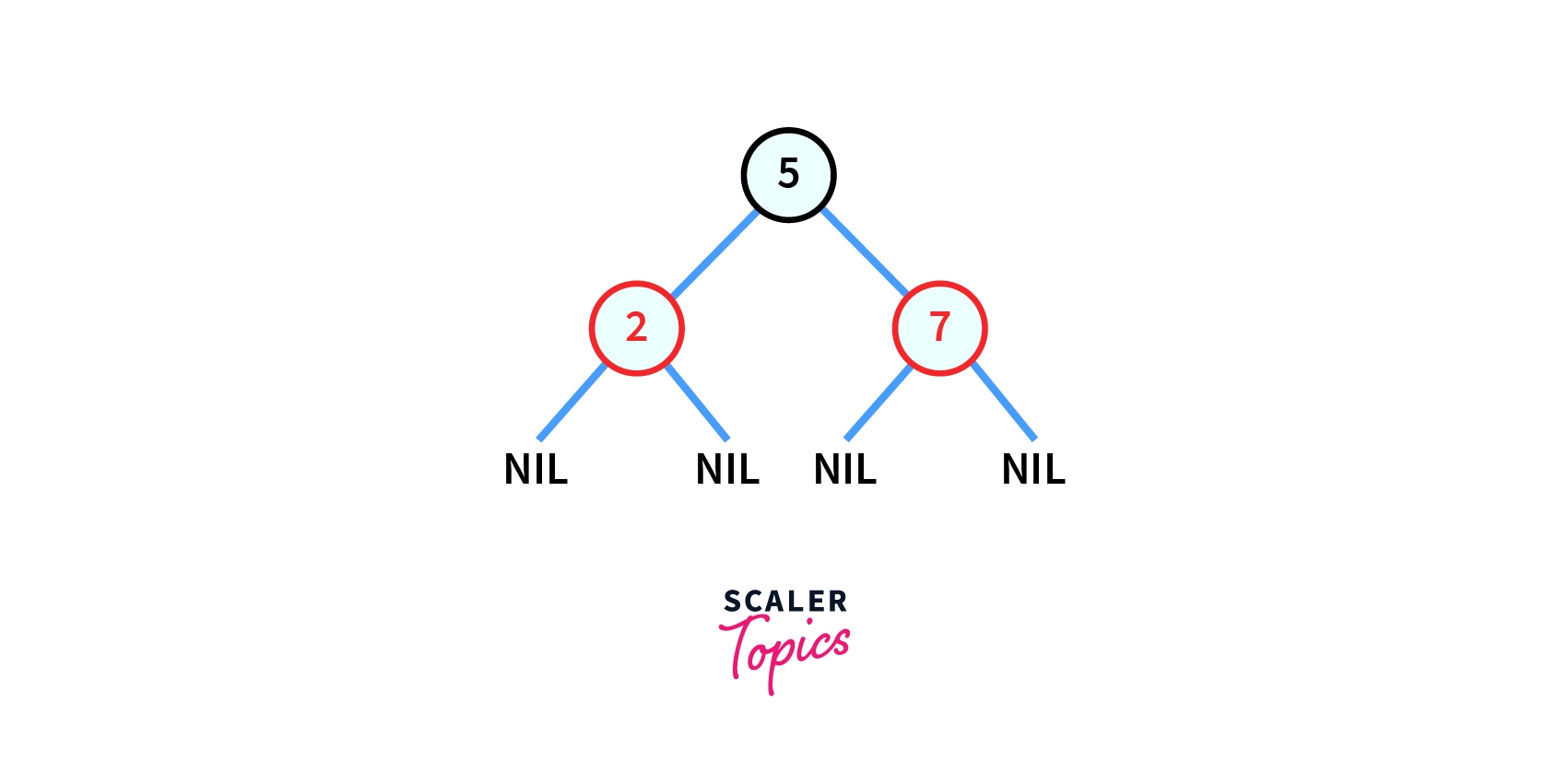In AVL trees we have seen how we are rotating the tree if the height of the tree is not balanced (difference between heights of left and right subtree is greater than 1), similarly rotations are also made in a red-black tree along with an additional step $i.e.$ recoloring of nodes to guarantee logarithmic time complexity.

Interestingly as each node requires only 1-bit data to store information about its color, the memory footprint of red-black trees are almost similar to classical (uncolored) binary trees.

Properties of Red Black Tree

A red-black tree follows all the properties of a binary search tree $i.e.$ "every node in the left subtree have a smaller value than root node and all the nodes in the right subtree have a larger value than root node and the same applies for all the subtrees." Additionally, all the red-black trees must follow the underlying properties -

• Every node should have a color (either RED or BLACK).
• The root node of the tree is always BLACK in color.
• All the leaf nodes of the tree are also BLACK in color.
• There can't be two adjacent nodes of RED color, $i.e.$ RED node can't have a RED colored parent/child.
• Every path from any node to any of its descendant NULL nodes must have an equal number of BLACK nodes.

Example of Red Black Tree

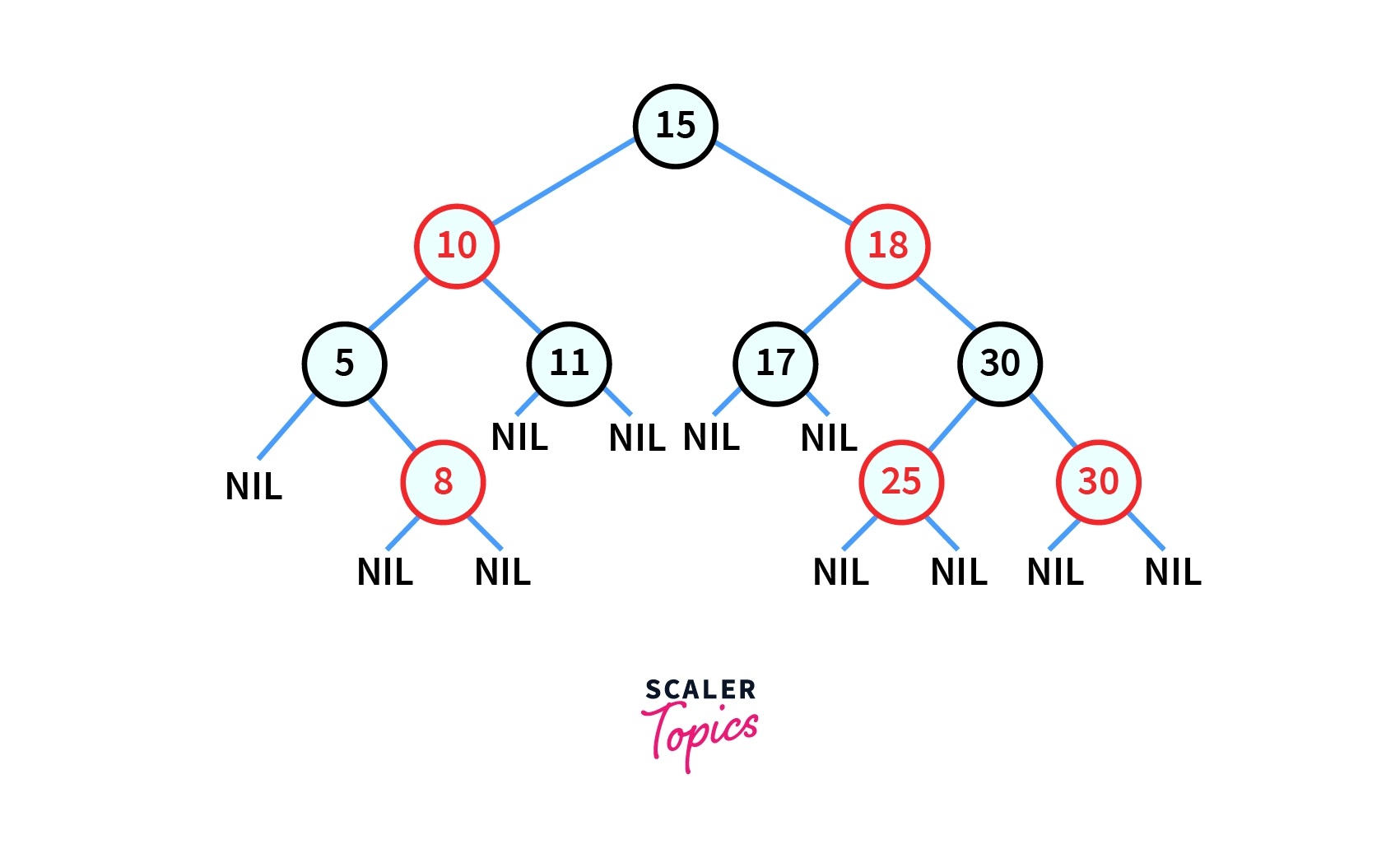In the above image, a red-black tree is represented. It is noticeable that it follows all the properties of a BST along with the exclusive properties of a red-black tree (listed above).

You can notice that the root node is BLACK, there are no two adjacent RED nodes and the same number of BLACK nodes are present from any node to its descendant NULL node.

Why Red Black Trees?

All the operations in Binary Search Trees cost $O(h)$ time to perform, where $h$ is the height of the tree which in the worst case (Skewed Tree) can go up to $n$ as shown below -

Hence, if somehow we can place an upper bound on the maximum height of the tree we can achieve good time complexity to perform operations in a red-black tree.

Since we can guarantee that at any instance of time the height of the red-black tree will be $O(log(n))$ therefore we can place an upper bound of $O(log(n))$ on the time complexity of the search, insert, and delete operations.

But the same upper bound can also be achieved with AVL trees, so why do we even need red-black trees? The answer is, AVL trees will cause more number of rotations during inserting and deleting. So it is advisable to use red-black trees when we have a large number of insert/delete operations to be performed.

Comparision with AVL Tree

While both Red-Black trees and AVL trees are self-balancing binary search trees, they vary in their approach towards maintaining balance, thereby leading to different performance characteristics. AVL trees provide faster lookup times due to their stricter adherence to balance, ensuring that the difference in the height of the left and right sub-trees of any node does not exceed 1. On the other hand, Red-Black trees allow for faster insertions and deletions since they're less rigid about balance, permitting a greater height difference. Consequently, AVL trees are preferred when the task involves more frequent lookups, while Red-Black trees are better suited for situations with many insertions and deletions.

Black Height of Red-black trees

Black height of a node is defined as the number of black nodes on any path from the node (not inclusive) to its leaf nodes (null nodes, which are also black). This includes any black nodes encountered along that path but does not count the red nodes. By definition, every path from a node to its descendant leaves has the same number of black nodes, helping to maintain the tree's balanced structure. This property is critical in maintaining approximately log2(n) height in Red-Black trees, ensuring efficient searching, insertion, and deletion operations.

Basic Operation in Red-black Trees

• Search: This operation involves traversing the tree from the root to the leaf nodes, following the correct path based on whether the key is less than or greater than the node's key. Since Red-Black trees are balanced, the time complexity of search operation is O(log n).
• Insertion: When a new node is inserted, the tree might become unbalanced, violating the Red-Black tree properties. Therefore, the tree is restructured and recolored via rotation operations to restore balance. Despite these additional steps, the time complexity of insertion remains O(log n).
• Deletion: Similar to insertion, deleting a node might disrupt the tree balance. After the node is removed, rotations and recoloring are performed to maintain the Red-Black tree properties. The time complexity of deletion is also O(log n).

Searching in a Red Black Tree

A red-black tree is nothing but a Binary Search Tree with some additional conditions for inserting and deleting the nodes such that height remains balanced. So we can apply the same searching algorithm of searching in a normal BST to search for an element in a Red Black Tree.

Algorithm:

Let's say we are searching for a node with key $x$ in a red-black tree

1. Start from the root node of the given tree.

2. If $x$ is smaller than the root's key then recurse for the left subtree, else if $x$ is greater than root's key then recurse for the right subtree.

3. If $x$ is found anywhere in the tree, return True and return False in the other case.

Example

Let in the given red-black tree we want to search a node with value $25$ -

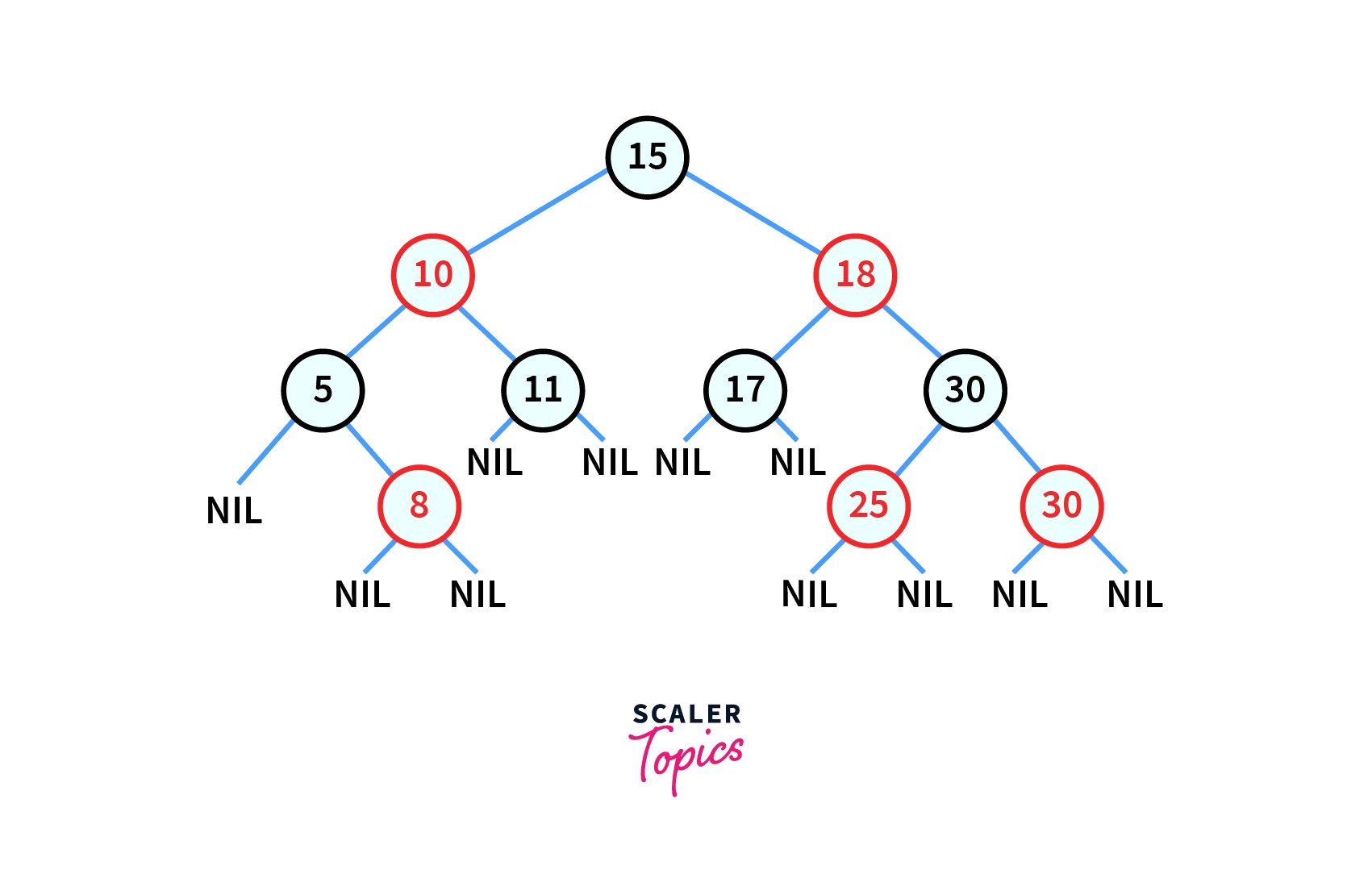Then according to the algorithm discussed above our flow of searching $25$ would be like -

PseudoCode

Codes

• C/C++

• Java

• Python

Time Complexity - $O(log(n))$, Since in the worst case (when $x$ do not exist in the tree) we will end up at a leaf position, which costs $O(h)$ time where $h=log(n)$.

Applications of Red Black tree -

• Almost all of the STL/library functions which use self-balancing BSTs (like map, set, multimap, multiset in C++, and TreeMap/TreeSet in Java) are using red-black trees internally.
• Completely Fair Scheduler (CPU scheduler used in Linux Kernel) is implemented using red-black trees.
• MySQL uses red-black trees for indexing of tables present in it.